Читайте также:
|
Идея всех методов спуска состоит в том, чтобы исходя из начального приближения - точки
Î Dn (Dn - область определения функции) перейти в следующую точку
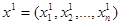Î D так, чтобы значение 
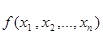уменьшилось, т.е. 
.
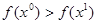Рассматриваем функцию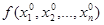 
при фиксированных значениях 
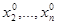как функцию одной переменной 
. Находим одним из описанных выше методов 
. Значение доставляющий минимум обозначаем 
. 
£
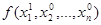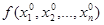
После нахождения точки минимума по координате переходим к нахождению минимума по координате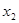 
от новой точки и так далее по всем оставшимся координатам.
Для гладких функций погрешность вычислений в данном методе складывается из погрешностей при вычислении минимума по каждой переменной, хотя для некоторых функций специального вида погрешность может быть и очень велика.
Центральным звеном рассматриваемого алгоритма является поиск минимума функции одной переменной. Методы применимые к этому случаю рассмотрены выше.
Дата добавления: 2015-08-27; просмотров: 65 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Численные методы поиска экстремумов функций многих переменных | | | Градиентный метод |