Условия применимости метода простых итераций.

Рассмотрим отображение n-мерного евклидова пространства в себя, заданное формулой: Y=AX+B, где А- матрица размерности nхn, X,B,Y ÎRⁿ. Главный вопрос применимости метода заключается в следующем: в каком случае это отображение будет сжимающим, т.е. существует некоторое число q, 0< q <1, такое что при всех х₁ и х₂ справедливо:

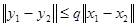
Что надо потребовать от матрицы А, чтобы выполнялось это условие?

Приведем несколько достаточных условий. Для этого вспомним, что основными нормами в пространстве Rⁿ являются

1. , где x=(x₁,x₂,...,x_n)

2.

3. 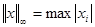, где i =1,2,...n

Рассмотрим в исходном пространстве векторов норму и оценим норму оператора преобразования Y=AX+B через элементы матрицы А.

Оценивать норму мы будем в два этапа: 1. Сначала оценим i -ую компоненту вектора y₁-y₂.

2. Затем оценим норму всего вектора y₁-y₂.

Возьмем i-ую компоненту вектора y₁-y₂ и оценим сверху эту разность по модулю.

Далее уже легко оценить и норму разности векторов y₁-y₂:

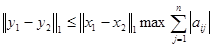, где максимум берется при всех i =1,2,…,n

Следствие. Если =мах <1, (i=1,2,…,n), то отображение Y=AX+B сжимающее.

Задача. Доказать, что для двух других норм в исходном пространстве получим:

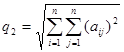, и , где максимум берется при всех j=1,2,…,n.

Если при этом хотя бы одно из этих чисел меньше 1, то отображение сжимающее.

Дата добавления: 2015-08-27