|
Читайте также: |
Как было уже сказано, в общем случае функция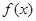 
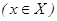может иметь несколько экстремумов (минимумов или максимумов). Задача поиска экстремумов сводится к их локализации и уточнению значений 
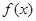и в точке экстремума. Все рассмотренные ниже численные методы предполагают, что локализация экстремумов каким-либо образом произведена (например, графически или аналитически) и задача численных методов будет состоять в уточнении полученных результатов с заданной точностью e. В дальнейшем для функций одной переменной под экстремумом будем подразумевать минимум 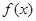. Будем считать, что Î[a,b], где a и b границы интервала поиска. В пределах отрезка [a,b] функция 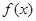необязательно непрерывная, могут существовать разрывы первого рода. Достаточно чтобы функция 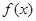на отрезке [a, b] была унимодальной, то есть, содержащей на указанном отрезке один минимум.
Дата добавления: 2015-08-27; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Численные методы решения экстремальных задач | | | Метод равномерного поиска. |