
Читайте также:
|
Этот метод основан на замене 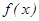 в промежутке
в промежутке 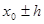 квадратичной параболой, экстремум которой вычисляется аналитически. После приближенного нахождения экстремума
квадратичной параболой, экстремум которой вычисляется аналитически. После приближенного нахождения экстремума  (максимума или минимума) можно задать
(максимума или минимума) можно задать  и повторить поиск. Таким образом, с помощью итерационной процедуры значение
и повторить поиск. Таким образом, с помощью итерационной процедуры значение  уточняется до получения его с заданной точностью
уточняется до получения его с заданной точностью 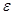 .
.
Алгоритм метода следующий:
1. Задаем начальное приближение 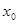 для
для  и вычисляем два смежных значения аргумента
и вычисляем два смежных значения аргумента 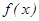
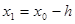 и
и 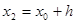 , где
, где  -полуинтервал поиска.
-полуинтервал поиска.
2. Вычисляем три значения  ,
,  ,
,  .
.
3. Находим коэффициенты параболы  , c (считая, что
, c (считая, что 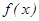 на указанном отрезке представляет собой параболу
на указанном отрезке представляет собой параболу  ) и по найденным коэффициентам вычисляем положение экстремума
) и по найденным коэффициентам вычисляем положение экстремума  .
.
4. Проверяем условие |x*-x0|<e. Если условие не выполняется, задаем x0=x* и идем к пункту 1. Если выполняется, считаем x* найденным с заданной точностью e, идем к пункту 5.
5. Выводим на печать x* и f(x*).
Упражнение 5. Вывести формулы пункта 3 алгоритма.
Дата добавления: 2015-08-27; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод деления отрезка пополам (или метод дихотомии). | | | Метод золотого сечения |