
|
Читайте также: |
Выразим целевую функцию через свободные переменные и допишем к задаче:
f = a0 -ar+1хr+1 -... -anхn.
Для базисного решения получим f =a0.
Перед нами стоит цель: уменьшить значение функции f за счет изменения свободных переменных. Свободные переменные для базисного решения равны 0, следовательно, мы можем их только увеличивать. Попробуем увеличивать хj, где r+1 £j £ n. Можем ли мы за счет увеличения этой свободной переменной уменьшить значение целевой функции? Если aj, положительное, то f уменьшается, а если aj отрицательное или 0, то нет. Т.е. если aj отрицательное, то нет смысла увеличивать хj, и наоборот.
Итак, если все aj отрицательны, то данное базисное решение является оптимальным, а минимум целевой функции f равен a0.
Как перейти от одного базисного решения к другому, более хорошему? Пусть есть такое j, что aj >0. При этом можно улучшить целевую функцию за счет увеличения хj. Все остальные свободные переменные оставляем равными 0. Тогда имеем:
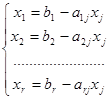
Посмотрим, до какой степени можно увеличивать хj. Для этого надо определить, что происходит при этом с базисными переменными. Если коэффициент аij не положителен, то значение xi при увеличении xj тоже растет и это не препятствует неограниченному росту xj.
Если получилось, что в выбранном столбце все aij<=0, то задача поставлена некорректно, а оптимального решения не существует, поскольку можно бесконечно увеличивать х(j) и вместе с ним бесконечно уменьшать значение целевой функции, а решение все время будет оставаться допустимым.
Пусть среди аij есть положительные числа. Тогда при возрастании хj будут уменьшаться соответствующие базисные переменные xi. При этом увеличивать хj можно до тех пор, пока первая из переменных х1, х2...,хr обратится в 0. Это произойдет, когда хj примет значение минимальной из величин bi/аi,j, у которых aij>0. После этого значение переменной хj станет отлично от 0,а какая-то из переменных хi обратится в 0. Это означает, что на очередном шаге мы переменную хj переводим в базисные, а хi - в свободные.
Алгоритм симплекс-метода:
1. Заполняем исходную таблицу (считается, что исходный базис найден).
2. Ищем в нижней строке максимальный положительный элемент (кроме a0). Если таких нет, то задача решена. Пусть aj - максимальное положительное число в нижней строчке.
3. В j-том столбце ищем положительные коэффициенты аkj (если таких нет, то задача не имеет решения). Во вспомогательный столбец заносим bk/аkj. Пусть минимальный элемент во вспомогательном столбце находится в i-й строке. На пересечении разрешающего столбца (j) и разрешающей строки (i) находится разрешающий элемент aij.
4. Заполняем новую таблицу в следующем порядке:
a) заголовок;
b) первый столбец (вместо хi пишем хj);
c) единичные столбцы;
d) разрешающую строку (делим на аij);
e) остальные строчки по порядку.
5. Возвращаемся к пункту 2.
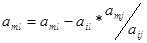 |
Дата добавления: 2015-08-27; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СИМПЛЕКС - МЕТОД | | | Пример. |