Пример. Решим с помощью симплекс-метода задачу:

Решим с помощью симплекс-метода задачу:

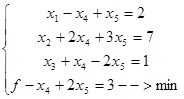
Видно, что данная система решена относительно свободных переменных х4 и х5 и свободных при базисных переменных х1, х2 и х3. Заполняем исходную симплекс-таблицу и действуем далее по алгоритму.

Базис	Свободные члены	х1	х2	х3	х4	х5	Вспомогательный столбец
х1					-1		2 <- минимум
х2							7/3
х3						-2
f					-1

Базисное решение (2,7,1,0,0) f=3

Базис	Свободные члены	х1	х2	х3	х4	х5	Вспомогательный столбец
х5					-1
х2		-3					0.2 <- минимум
х3					-1
f	-1	-2

Базисное решение (0,1,5,0,2) f= -1

Базис	Свободные члены	х1	х2	х3	х4	х5	Вспомогательный столбец
х5	2.2	0.4	0.2
х4	0.2	-0.6	0.2
х3	5.2	1.4	0.2
f	-1.2	-1.4	-0.2

Базисное решение (0,0,5.2,0.2,2.2) f= -1.2

Видим, что данная таблица является последней и соответствующее ей базисное решение является оптимальным. Ответ получаем такой: fmin =-1.2, вектор X=(0;0;5.2;0.2;2.2).

Содержание лабораторной работы.

1. Ответить на вопросы контролирующей программы.

2. Решить. предложенный вариант задачи графическим способом

3. Решить предложенный вариант задачи симплекс-методом, используя графическое решение для контроля правильности вычислений.

4. Составить, отладить и протестировать на контрольных примерах программу решения задачи линейного программирования симплекс-методом.

5. Составить отчет, содержащий цель и назначение работы, постановку задачи и текст программы.

Дата добавления: 2015-08-27