Оценка премии европейского опциона

Иностранную валюту можно рассматривать как акцию, для ко- торой известна ставка дивиденда. Иностранная валюта приносит владельцу доходность, то есть ставку дивиденда, равную ставке без риска в иностранной валюте. Поэтому для оценки премии опцио- нов на валюту можно воспользоваться формулами Блэка-Сколеса для европейских опционов на акции с известной ставкой дивиден- да, а именно:

ce = Se

- rT

N (d 1)- Xe

- rT

N (d 2)

pe = Xe

- rT

N (- d 2)- Se

rjT

N (- d 1)

ln(S

d 1 =

X)+(r - r +σ 2 2) T

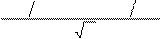σ T

d 2 =

ln(S

X)+(r - rj - σ 2 2) T

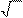= d 1 -σ T

σ T

S — цена (курс) единицы иностранной валюты в национальной валюте (например, для США курс канадского доллара, выражен- ный в американских долларах);

rf — ставка без риска для иностранной валюты.

Дата добавления: 2015-08-27