|
Читайте также: |
Блэк и Сколес вывели следующие формулы оценки премии опционов
ce = SN (d 1)- Xe
- rT
N (d 2)
(48)
Поскольку се = са, то данная формула позволяет определить премию и американского опциона.
pe = Xe
- rT
N (- d 2)- SN (- d 1)
(49)
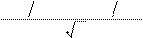d ln(S
X)+(r +σ 2 2) T
ln(S
X)+ rT
1 σ T
1 = σ T
= +
σ T 2
(50)
172
ln(S
d 2 =
X) + (r + σ 2 2) T
= d 1 -s T
(51)
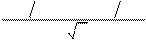σ T
с — стандартное отклонение цены акции.
В формулах Блэка-Сколеса величина а берется в годовом исчис- лении. В аналитических материалах стандартное отклонение дает- ся в процентах, в формулы она подставляется в десятичных значениях
r — ставка без риска; на практике в формулы подставляется существующая ставка без риска для инвестиций, которые осуще- ствляются на время Т;
N (di) — функция распределения, показывающая вероятность того, что нормированная нормальная переменная будет меньше di.
Пример. S = 50 долл., =45 долл., r = 10%, T= 6 месяцев,
σ= 0,525. Необходимо определить премию опциона колл.
ln(50 45)+0,1´0,5
d 1 = +0,5 ´0,525 ´
0,5 =0,6041
0,525 ´
0,5
d 2 =0,6041 -0,525 ´
0,5 = 60,2329
Из таблицы значений функции N (di)(cм. приложение 2) нахо-
дим:
Тогда
N(d1) = 0,7271; N(d2) = 0,5921
се = 50 долл. ´ 0,7271 – 45 долл. е-0,1´0,5´0,5921 = 11,01 долл.
б) Определение премии опционов на акции,
Дата добавления: 2015-08-27; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление исторического стандартного отклонения | | | Выплачивающие дивиденды |