Выплачивающие дивиденды

Как уже отмечалось выше, информация о дивидендах может быть задана в двух формах: в виде 1) ставки дивиденда и 2) как абсолютное значение дивиденда. Рассмотрим вначале вопрос оп- ределения премии опциона для первого варианта.

Для такого случая дивиденд рассматривается как непрерывно начисляемый дивиденд. Соответственно ставка дивиденда пред- ставляет собой непрерывно начисляемый процент. Если ставка дивиденда меняется в рамках рассматриваемого периода, то для расчетных целей можно использовать ее среднюю величину в рас- чете на год. Как известно, выплата дивиденда вызывает падение курса акции на величину дивиденда. Сравним динамику роста курсовой стоимости двух акций за некоторый период Т. В конце этого периода на первую акцию выплачивается дивиденд, а на

вторую — не выплачивается. Тогда мы можем сказать, что темп прироста курсовой стоимости первой акции ниже на величину q или что темп прироста курсовой стоимости второй акции будет выше на величину q.

Если в начале периода T курс акции, выплачивающей дивиденд,

равен S, то в конце этого периода она будет стоить столько же, сколько и акция, не выплачивающая дивиденда, которая в начале периода стоит S e-qT. Поэтому можно сделать вывод о том, что европейский опцион для первой и второй акции должен иметь одинаковую стоимость. Выше мы уже привели формулы Блэка- Сколеса для оценки премии европейских опционов. Данные фор-

мулы применимы и для опционов на акции, выплачивающие дивиденд, с той только разницей, что место S займет величина S e-qT

ce = Se

- qT

N (d 1)- Xe

- rT

N (d 2)

(52)

pe = Xe

- rT

N (- d 2)- Se

- qT

N (- d 1)

(53)

ln(S

d 1 =

X) + (r - q + σ 2 2) T

(54)

σ T

d 2 =

ln(S

X) + (r - q - σ 2 2) T

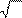= d 1 - σ T

(55)

σ T

d1 и d2 принимают указанный вид вследствие следующего пре-

образования:

ln Se

- qT

=ln S

- qT

X X

Этот результат впервые получил Мертон.

Если инвестор имеет информацию об абсолютном размере ди-

виденда, то величина S уменьшается на приведенную стоимость дивиденда, а значение σ принимается как стандартное отклонение чистой цены акции. Полученные цифры подставляются в формулы Блэка-Сколеса.

Дата добавления: 2015-08-27