
Читайте также:
|
Если уравнение  , где
, где  - дифференцируемая функция по переменным
- дифференцируемая функция по переменным  , определяет
, определяет  как функцию независимых переменных
как функцию независимых переменных  , то частные производные этой неявной функции
, то частные производные этой неявной функции 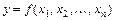 вычисляются по формулам:
вычисляются по формулам:  ,
,  ,…,
,…,  при условии, что
при условии, что  .
.
В частности, для функции  , заданной неявно уравнением
, заданной неявно уравнением  справедлива формула
справедлива формула  , при условии
, при условии  , а для функции
, а для функции  , заданной уравнением
, заданной уравнением 
справедливы формулы:  ,
,  , при условии
, при условии  .
.
Частные производные высших порядков вычисляются последовательным дифференцированием данных формул.
Уравнение касательной плоскости к поверхности  , заданной неявным уравнением
, заданной неявным уравнением  , в точке
, в точке  имеет вид
имеет вид  , а уравнение нормали – вид
, а уравнение нормали – вид  .
.
Тема 6. Экстремумы функций нескольких переменных.
Точка  , принадлежащая области определения
, принадлежащая области определения 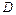 функции
функции  , называется стационарной точкой функции, если в этой точке каждая из её частных производных равна нулю, т.е.
, называется стационарной точкой функции, если в этой точке каждая из её частных производных равна нулю, т.е.  ,…,
,…,  или
или  .
.
Точка  называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции  , если существует окрестность точки
, если существует окрестность точки  такая, что для всех точек
такая, что для всех точек  этой окрестности выполняется неравенство
этой окрестности выполняется неравенство  (
( ).
).
Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Необходимое условие экстремума. Если  - точка локального экстремума функции
- точка локального экстремума функции  , дифференцируемой в точке
, дифференцируемой в точке  , то
, то  - стационарная точка функции.
- стационарная точка функции.
Достаточное условие экстремума. Пусть  - стационарная точка дважды дифференцируемой в точке
- стационарная точка дважды дифференцируемой в точке  функции
функции  . Тогда, если при всевозможных наборах значений
. Тогда, если при всевозможных наборах значений  , не равных одновременно нулю:
, не равных одновременно нулю:
1)  , то в точке
, то в точке  функция
функция  имеет максимум; 2)
имеет максимум; 2) 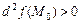 , то в точке
, то в точке  функция имеет минимум; 3)
функция имеет минимум; 3)  принимает как положительные, так и отрицательные значения, то в точке
принимает как положительные, так и отрицательные значения, то в точке  функция
функция  не имеет экстремума.
не имеет экстремума.
Исследование знака  сводится к исследованию знакоопределённости второго дифференциала, как квадратичной формы относительно переменных
сводится к исследованию знакоопределённости второго дифференциала, как квадратичной формы относительно переменных  (например, с помощью критерия Сильвестра).
(например, с помощью критерия Сильвестра).
В частности, функция  в стационарной точке
в стационарной точке 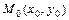 , при условии
, при условии  , где
, где  ,
,  ,
,  : 1) имеет максимум, если
: 1) имеет максимум, если  и
и  ; 2) имеет минимум, если
; 2) имеет минимум, если  и
и  ; 3) не имеет экстремума, если
; 3) не имеет экстремума, если  .
.
Точка  называется точкой условного минимума (максимума) функции
называется точкой условного минимума (максимума) функции  , если существует окрестность точки
, если существует окрестность точки  такая, что для всех точек
такая, что для всех точек  этой окрестности, удовлетворяющих уравнениям связи
этой окрестности, удовлетворяющих уравнениям связи  (
( ) выполняется неравенство
) выполняется неравенство  (
( ). Точки условного минимума и максимума функции называются точками условного экстремума, а значения функции в этих точках – условными экстремумами функции.
). Точки условного минимума и максимума функции называются точками условного экстремума, а значения функции в этих точках – условными экстремумами функции.
Задача нахождения условного экстремума сводится к нахождению обычного экстремума функции Лагранжа  , где
, где  (
( ) –постоянные множители Лагранжа.
) –постоянные множители Лагранжа.
Необходимое условие условного экстремума. Если  - точка условного экстремума функции
- точка условного экстремума функции  при наличии уравнений связи
при наличии уравнений связи  (
( ), то в точке
), то в точке  выполняются условия
выполняются условия
 .
.
Решая данную систему, находят неизвестные координаты точки  , в которой возможен условный экстремум и соответствующие ей значения множителей Лагранжа
, в которой возможен условный экстремум и соответствующие ей значения множителей Лагранжа  .
.
Вопрос о существовании и характере условного экстремума решается на основании изучения (например, с помощью критерия Сильвестра) знака второго дифференциала функции Лагранжа  в точке
в точке  при значениях
при значениях  , рассматриваемого как квадратичная форма относительно переменных
, рассматриваемого как квадратичная форма относительно переменных  при условии, что они связаны соотношениями:
при условии, что они связаны соотношениями:  (
( ).
).
В частности, для функции  исследуется знак
исследуется знак 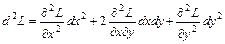 при условии
при условии  .
.
Достаточное условие условного экстремума. Пусть  - точка возможного условного экстремума функции
- точка возможного условного экстремума функции  , т.е. в этой точке выполнены необходимые условия условного экстремума. Тогда, если при всевозможных наборах значений
, т.е. в этой точке выполнены необходимые условия условного экстремума. Тогда, если при всевозможных наборах значений  , удовлетворяющих соотношениям
, удовлетворяющих соотношениям  (
( ) и не равных одновременно нулю: 1)
) и не равных одновременно нулю: 1)  , то в точке
, то в точке  функция
функция  имеет условный максимум; 2)
имеет условный максимум; 2) 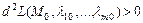 , то в точке
, то в точке  функция имеет условный минимум; 3)
функция имеет условный минимум; 3)  принимает как положительные, так и отрицательные значения, то в точке
принимает как положительные, так и отрицательные значения, то в точке  функция
функция  не имеет условного экстремума.
не имеет условного экстремума.
Если функция  дифференцируема в ограниченной и замкнутой области, то она достигает своих наибольшего и наименьшего значений в этой области или в стационарной точке, или в граничной точке области.
дифференцируема в ограниченной и замкнутой области, то она достигает своих наибольшего и наименьшего значений в этой области или в стационарной точке, или в граничной точке области.
Дата добавления: 2015-07-25; просмотров: 234 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные правила дифференцирования элементарных функций. | | | Неопределенный интеграл |