
Читайте также:
|
1) Находим область определения функции:  =
=  ).
).
2) Поскольку данная функция является элементарной, то областью её непрерывности является область определения  , а точками разрыва являются точки
, а точками разрыва являются точки  и
и 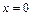 , не принадлежащие множеству
, не принадлежащие множеству  , но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках
, но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках  и
и 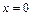 , вычислив в них односторонние пределы функции:
, вычислив в них односторонние пределы функции:
 ,
,  ,
,
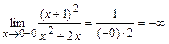 ,
,  .
.
Так как односторонние пределы функции в точках  и
и 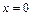 - бесконечные, то данные точки являются точками бесконечного разрыва.
- бесконечные, то данные точки являются точками бесконечного разрыва.
3) Функция не является периодической.
Функция  , в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
, в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
Проверяем является ли функция чётной или нечётной. Так как область определения функции  =
=  ) не симметрична относительно точки
) не симметрична относительно точки 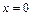 , то данная функция – общего вида.
, то данная функция – общего вида.
4) Находим точки пересечения графика с осями координат.
Так как  , то точек пересечения графика с осью
, то точек пересечения графика с осью  нет.
нет.
Положим 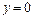 и решим уравнение
и решим уравнение  . Его решением является
. Его решением является  . Следовательно, точка
. Следовательно, точка  - точка пересечения графика с осью
- точка пересечения графика с осью  .
.
5) Находим вертикальные и наклонные асимптоты графика функции.
Прямая  является вертикальной асимптотой, тогда и только тогда, когда
является вертикальной асимптотой, тогда и только тогда, когда 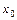 является точкой бесконечного разрыва функции
является точкой бесконечного разрыва функции  .
.
Так как точки  и
и 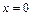 - точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые
- точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые  и
и 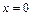 .
.
Прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  при
при  тогда и только тогда, когда одновременно существуют конечные пределы:
тогда и только тогда, когда одновременно существуют конечные пределы: 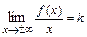 и
и 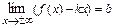 .
.
Вычисляем сначала пределы при  :
:  ,
, 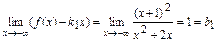 .
.
В дальнейшем будем иметь в виду следующий часто встречающийся предел: 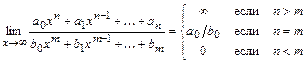
Следовательно  , т.е.
, т.е.  - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
Аналогично вычисляем пределы при  :
: 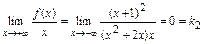 ,
,  Следовательно
Следовательно  , т.е.
, т.е.  - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
6) Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:



и определяем критические точки функции  , т.е. точки
, т.е. точки  в которых
в которых  или
или  не существует:
не существует:

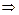

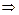
 ;
;
 не существует при
не существует при 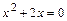
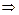
 и
и  .
.
Таким образом, единственной критической (стационарной) точкой функции  является точка
является точка  .
.
Исследуем знак производной  в интервалах, на которые критические точки функции
в интервалах, на которые критические точки функции  разбивают её область определения
разбивают её область определения  , и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
, и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:

| 
| 
| 
| 
| 
|

| + | + | 
| 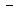
| 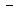
|

| возрастает | возрастает | 
| убывает | убывает |
Так как при переходе слева направо через точку  производная
производная  меняет знак с «+» на «
меняет знак с «+» на «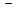 », то точка
», то точка  является точкой локального максимума и
является точкой локального максимума и 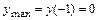 .
.
7) Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:
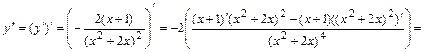

и определяем точки возможного перегиба  , т.е. точки
, т.е. точки  в которых
в которых  или
или  не существует:
не существует:  , так как
, так как 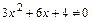 (квадратное уравнение не имеет действительных корней);
(квадратное уравнение не имеет действительных корней);  не существует при
не существует при 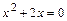
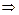
 и
и  .
.
Таким образом, функция  не имеет точек возможного перегиба.
не имеет точек возможного перегиба.
Исследуем знак второй производной  в интервалах, на которые точки возможного перегиба функции
в интервалах, на которые точки возможного перегиба функции  разбивают её область определения
разбивают её область определения  , и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим следующей таблицей:
, и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим следующей таблицей:

| 
| 
| 
|

| + | 
| + |

| график вогнутый | график выпуклый | график вогнутый |
Точек перегиба нет.
8) На основании полученных результатов строим график функции (рис.3)
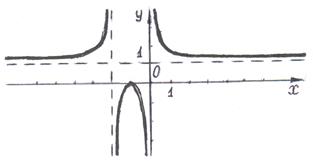
Рис.3.
Ответ: Рис.3.
5.1-30. Для указанной функции  требуется найти наибольшее и наименьшее значения функции на отрезке
требуется найти наибольшее и наименьшее значения функции на отрезке 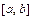 :
:
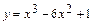 ,
, 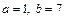 .
.
Наибольшее и наименьшее значения функции 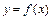 непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке
непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке  достигается или в точках
достигается или в точках  , в которых
, в которых  или
или  не существует, или на концах отрезка.
не существует, или на концах отрезка.
1) Находим первую производную функции:

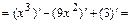

и определяем внутренние критические точки функции  , т.е. точки
, т.е. точки  в которых
в которых  или
или  не существует:
не существует:

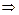
 , точек
, точек  в которых
в которых  не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции
не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции  на отрезке
на отрезке  является точка
является точка  .
.
2) Вычисляем значения функции  во внутренних критических точках и на концах отрезка
во внутренних критических точках и на концах отрезка  :
:  ,
,  ,
, 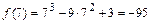 .
.
3) Сравниваем значения 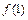 ,
,  ,
,  и находим наименьшее и наибольшее значения функции
и находим наименьшее и наибольшее значения функции  на отрезке
на отрезке  :
:
 ,
,  .
.
Ответ:  ,
, 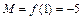
6.1 – 30. Для указанной функции  требуется: а) найти полный дифференциал
требуется: а) найти полный дифференциал  ; б) вторую частную (смешанную) производную
; б) вторую частную (смешанную) производную  ; если
; если  .
.
Полный дифференциал функции  имеет вид
имеет вид 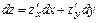 .
.
Частные производные функции  вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу
вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу  (аргументу
(аргументу  ), то другой аргумент
), то другой аргумент  (аргумент
(аргумент  ) считается постоянным.
) считается постоянным.
Решение.
а) Находим частные производные первого порядка  и
и  функции
функции
 :
: 




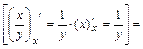
 ;
;

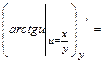



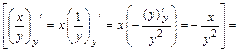
 .
.
Тогда полный дифференциал  функции имеет вид:
функции имеет вид:
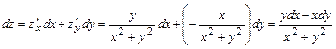 .
.
б) Вторую частную производную 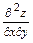 (или кратко
(или кратко  ) находим как первую частную производную по аргументу
) находим как первую частную производную по аргументу  от функции
от функции  :
:



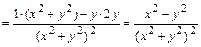 .
.
Ответ: а) 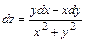 , б)
, б) 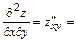
 ;
;
7.1 – 30. Для функции  , заданной неявно, найти частные производные
, заданной неявно, найти частные производные  и
и  .
.
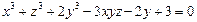
Для функции  , заданной уравнением
, заданной уравнением  справедливы формулы:
справедливы формулы:  ,
,  , при условии
, при условии  .
.
В данном примере  . Найдем частные производные функции
. Найдем частные производные функции  :
:
 ;
;
 ;
;
 ;
;
Тогда, учитывая что  ,
,  , получим:
, получим:
 ;
;

Дата добавления: 2015-07-25; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| А) ; б) ; в) . | | | Ответ: а) ,б) . |