
Читайте также:
|
6.1. 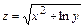 , 6.2.
, 6.2.  ,
,
6.3. 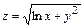 , 6.4.
, 6.4.  ,
,
6.5. 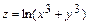 , 6.6.
, 6.6. 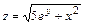 , 6.7.
, 6.7.  , 6.8.
, 6.8. 
6.9.  6.10.
6.10. 
6.11.  6.12.
6.12. 
6.13. 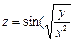 6.14.
6.14. 
6.15.  6.16.
6.16. 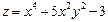
6.17.  6.18.
6.18. 
6.19.  6.20.
6.20. 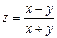
6.21.  6.22.
6.22. 
6.23. 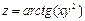 6.24.
6.24. 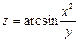
6.25. 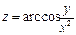 6.26.
6.26. 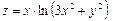
6.27. 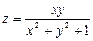 6.28.
6.28. 
6.29.  6.30.
6.30. 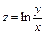
7. Для функции  , заданной неявно, найти частные производные
, заданной неявно, найти частные производные  и
и  .
.
7.1  7.2.
7.2. 
7.3.  7.4.
7.4. 
7.5. 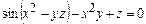 7.6.
7.6. 
7.7. 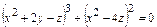 7.8.
7.8. 
7.9.  7.10.
7.10.  7.11.
7.11.  7.12.
7.12. 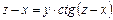 7.13.
7.13. 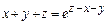 7.14.
7.14.  7.15.
7.15.  7.16.
7.16.  7.17.
7.17.  7.18.
7.18.  7.19.
7.19.  7.20.
7.20.  7.21.
7.21.  7.22.
7.22. 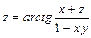 7.23.
7.23. 
7.24. 
7.25. 
7.26. 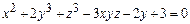
7.27. 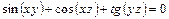 7.28.
7.28.  7.29.
7.29.  7.30.
7.30. 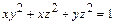
8. Найти локальные экстремумы функции 
8.1.  8.2.
8.2. 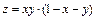 ,
, 
8.3. 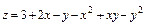 8.4.
8.4. 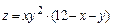 ,
, 
8.5.  ,
,  8.6.
8.6. 
8.7. 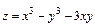 8.8.
8.8. 
8.9. 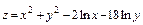 8.10.
8.10. 
8.11. 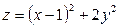 . 8.12.
. 8.12. 
8.13. 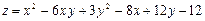 8.14.
8.14. 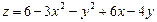
8.15.  8.16.
8.16. 
8.17.  8.18.
8.18. 
8.19.  8.20.
8.20. 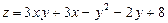
8.21.  8.22.
8.22. 
8.23. 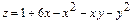 8.24.
8.24. 
8.25. 
8.26.  8.27.
8.27. 
8.28.  8.29.
8.29. 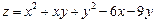
8.30. 
9. Найти условные экстремумы функции  (методом Лагранжа):
(методом Лагранжа):
9.1.  при
при 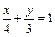
9.2.  при
при 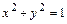
9.3.  при
при 
9.4.  при
при 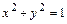
9.5.  при
при 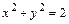
9.6.  при
при 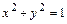
9.7.  при
при 
9.8.  при
при 
9.9.  при
при 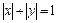
9.10. 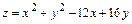 при
при 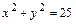
9.11.  при
при 
9.12.  при
при 
9.13.  при
при 
9.14.  при
при 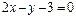
9.15. 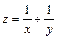 при
при 
9.16.  при
при 
9.17.  при
при 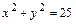
9.18.  при
при 
9.19.  при
при 
9.20.  при
при 
9.21.  при
при 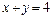
9.22. 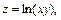 при
при 
9.23.  при
при 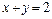
9.24.  при
при 
9.25.  при
при 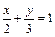
9.26.  при
при 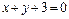
9.27. 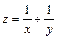 при
при 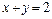
9.28. 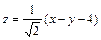 при
при 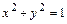
9.29.  при
при 
9.30.  при
при 
10. Найти наибольшее и наименьшее значения функции  в ограниченной и замкнутой области D:
в ограниченной и замкнутой области D:
10.1.,.
10.2.,.
10.3.,.
10.4.,.
10.5..
10.6.,.
10.7.,.
10.8.,.
10.9.,.
10.10.,.
10.11.,.
10.12.,.
10.13.,.
10.14.,.
10.15.,.
10.16.,.
10.17.,.
10.18.,.
10.19.,.
10.20.,.
10.21.,.
10.22.,.
10.23.,.
10.24.,.
10.25.,.
10.26.,.
10.27.,.
10.28.,.
10.29.,.
10.30.,.
11. Найти: а) координаты градиента функции  в точке
в точке 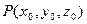 ; б) уравнения касательной плоскости и нормали к поверхности, заданной уравнением
; б) уравнения касательной плоскости и нормали к поверхности, заданной уравнением  в точке
в точке  .
.
11.1 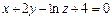 ,
, 
11.2.  ,
, 
11.3. 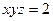 ,
, 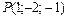
11.4. 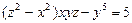 ,
, 
11.5.  ,
, 
11.6..  ,
, 
11.7..  ,
, 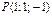
11.8.  ,
, 
11.9.  ,
, 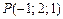
11.10. 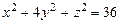 ,
, 
11.11.  ,
, 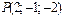
11.12.  ,
, 
11.13.  ,
, 
11.14.  ,
, 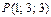
11.15. 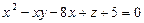 ,
, 
11.16. 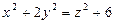 ,
, 
11.17. 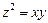 ,
, 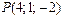
11.18. 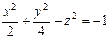 ,
, 
11.19. 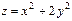 ,
, 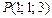
11.20. 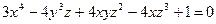 ,
, 
11.21.  ,
, 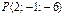
11.22. 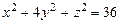 ,
, 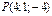
11.23.  ,
, 
11.24.  ,
, 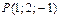
11.25.  ,
, 
11.26.  ,
, 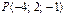
11.27.  ,
, 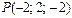
11.28. 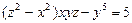 ,
, 
11.29. 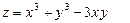 ,
, 
11.30..  ,
, 
Вопросы к экзамену (семестр 2).
Дата добавления: 2015-07-25; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Раздел I. Дифференциальное исчисление функции одной переменной. | | | Раздел I..Дифференциальное исчисление функции одной переменной. |