
Вычисление предела  , где
, где  , всегда начинают с подстановки в
, всегда начинают с подстановки в  предельного значения её аргумента
предельного значения её аргумента  . Если в результате получают неопределённость
. Если в результате получают неопределённость  или
или  , то для её раскрытия применяют правило Лопиталя:
, то для её раскрытия применяют правило Лопиталя:  , где
, где 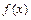 и
и  - функции, дифференцируемые в окрестности
- функции, дифференцируемые в окрестности  . В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:
. В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:  ,
,  ,
,  ,
, 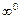 ,
, 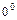 путём преобразований:
путём преобразований: 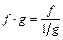 ,
, 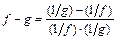 ,
, 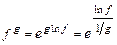 сводят к раскрытию неопределенностей вида
сводят к раскрытию неопределенностей вида  или
или 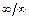 .
.
Решение.
а) 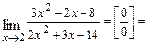
 , где
, где


 ,
,



Тогда 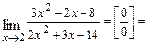
 .
.
б) 
 , где
, где




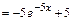 ,
,

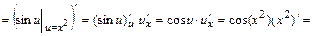
 .
.
Тогда 
 . Применяем правило Лопиталя ещё раз:
. Применяем правило Лопиталя ещё раз: 
 , где
, где


 ,
,

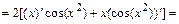
 =
= 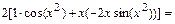
 .
.
Тогда 
 .
.
в)  . Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду
. Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду 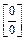 , после чего применим правило Лопиталя. Получим
, после чего применим правило Лопиталя. Получим 
= 
 , где
, где
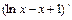

 ,
,


 .
.
Тогда 
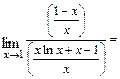
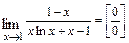 .
.
Применяем правило Лопиталя ещё раз:
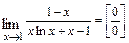
 , где
, где 

 ,
,



 .
.
В итоге получим 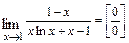
 .
.
Ответ:
а)  ; б)
; б)  ;в)
;в)  .
.
4.1-30. Для указанной функции  требуется провести полное исследование функции и построить её график:
требуется провести полное исследование функции и построить её график:
 ;
;
Для построения графика функции  нужно:
нужно:
1) найти область определения функции;
2) найти область непрерывности функции и точки разрыва;
3) исследовать функцию на чётность, нечётность и периодичность;
4) найти точки пересечения графика с осями координат;
5) найти асимптоты графика функции;
6) найти интервалы возрастания и убывания, экстремумы функции;
7) найти интервалы выпуклости, вогнутости и точки перегиба.
Дата добавления: 2015-07-25; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Решение. |