
Читайте также:
|
1. Приращение функции. Определение производной. Правая и левая производные. Условия существования конечной производной в точке.
2. Геометрический смысл производной. Касательная и нормаль к кривой в данной точке, их уравнения.
3. Понятие дифференцируемости функции в точке. Взаимосвязь понятий: дифференцируемость в точке, непрерывность в точке, существование в точке конечной производной.
4. Непосредственное нахождение производной. Простейшие правила дифференцирования (постоянной, суммы, разности, произведения и частного функций).
5. Дифференцирование обратной функции.
6. Дифференцирование сложной функции.
7. Дифференцирование функций, заданных параметрически.
8. Логарифмическая производная, её применение для нахождения производной степенно-показательной функции.
9. Дифференциал функции. Правила вычисления дифференциалов. Применение дифференциала в приближённых вычислениях.
10. Производные и дифференциалы высших порядков, их нахождение.
11. Теорема Ферма. Геометрический смысл теоремы.
12. Теорема Ролля. Геометрический смысл теоремы.
13. Теорема Лагранжа. Геометрический смысл теоремы. Формула конечных приращений Лагранжа.
14. Теорема Коши.
15. Формулы Тейлора и Маклорена, их применение в приближённых вычислениях.
16. Правило Лопиталя и его применение для раскрытия неопределённостей: 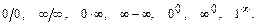
17. Достаточный признак монотонности функции. Стационарные и критические точки. Нахождение интервалов монотонности функции.
18. Точки локального экстремума (максимума и минимума) и локальные экстремумы функции. Необходимое и достаточные условия существования локального экстремума функции.
19. Глобальные экстремумы (наибольшее и наименьшее значения) функции на отрезке, их нахождение.
20. Понятия выпуклости и вогнутости функции. Достаточный признак выпуклости (вогнутости) функции на интервале. Нахождение интервалов выпуклости и вогнутости функции.
21. Точка перегиба графика функции, условия её существования и нахождение.
22. Понятие асимптоты графика функции. Вертикальные и наклонные асимптоты, условия их существования и нахождение.
Дата добавления: 2015-07-25; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Для указанной функции требуется: найти а)полный дифференциал ; б) смешанную производную . | | | Раздел II. Функции нескольких переменных. |