Решение.

а) , где

= ;

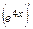
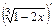
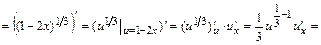
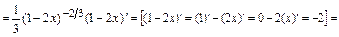
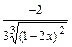
Тогда .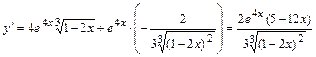

б) 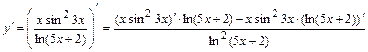, где

.

.

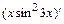
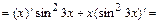
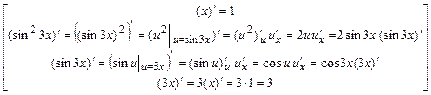
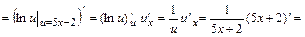
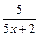Тогда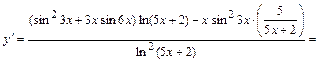

.

в)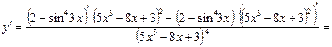

.

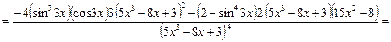
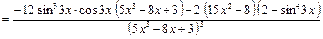Ответ: а) 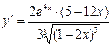б) .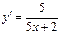

в)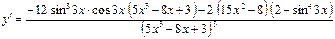

2.1-30. Найти а) производную функции , заданной параметрически; б) производную функции , заданной неявно.

а) Производную функции , заданной параметрическими уравнениями 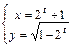находим по формуле 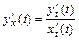, где

;

.

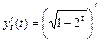
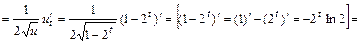
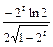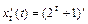
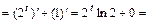
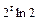Тогда .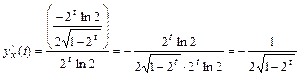

б) Уравнение 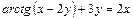неявно определяет функцию . Дифференцируя его по x, получим: .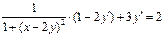

Выразим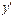

;

.

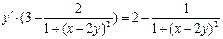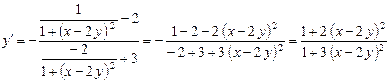Ответ: а) 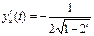б) .

3.1-30. Вычислить пределы, используя правило Лопиталя.

Дата добавления: 2015-07-25