Ответ: а) ,б) .

Тема 3. Исследование функций с помощью производных, построение их графиков. | Виды самостоятельной работы студентов. | Методические указания по изучению дисциплины. | Раздел I. Дифференциальное исчисление функции одной переменной. | Для указанной функции требуется: найти а)полный дифференциал ; б) смешанную производную . | Раздел I..Дифференциальное исчисление функции одной переменной. | Раздел II. Функции нескольких переменных. | Семестр 2. | Решение. | А) ; б) ; в) . |

Читайте также:

8.1 – 30. Найти локальные экстремумы функции

Для нахождения локальных экстремумов дифференцируемой функции необходимо: 1) Найти область определения функции. 2) Найти первые частные производные и функции. 3) Решить систему уравнений (необходимое условие экстремума) 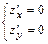и найти точки 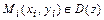(с учётом возможных дополнительных ограничений на значения аргументов и ) возможного локального экстремума функции. 4) Найти вторые частные производные , , 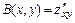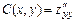; составить выражение и вычислить значения и 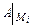в каждой точке возможного экстремума. 5) Сделать вывод о наличии экстремумов функции , используя достаточное условие экстремума: если , то в точке экстремума нет; если и , то в точке - локальный минимум; если и , то в точке - локальный максимум; если , то требуется дополнительное исследование точки (например, по определению). 6) Найти локальные экстремумы (экстремальные значения) функции.