Читайте также:
|
1) Находим область определения функции 
.
2) Находим первые частные производные 
и 
:
;
.
3) Составим систему уравнений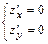 
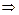
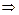
и решим её. Получим четыре решения: 
, 
, 
, 
. Из них точками возможного экстремума функции 
в области 
являются только две точки: 
и 
.
4) Находим вторые частные производные:
;
;
,
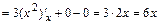составляем выражение 
и вычисляем:
; 
, 
.
5) Делаем вывод о наличии экстремумов. Так как:
, то в точке экстремума нет;
, 
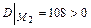, то в точке - локальный минимум.
6) Находим локальный минимум
.
Дата добавления: 2015-07-25; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ответ: а) ,б) . | | | Найти условные экстремумы функции приусловии . |