Найти условные экстремумы функции приусловии .

Читайте также:

Для нахождения методом Лагранжа локальных экстремумов дифференцируемой функции при условии необходимо: 1) Найти область определения функции. 2) Составить функцию Лагранжа 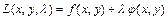, где - неопределённый постоянный множитель Лагранжа. 3) Решить систему уравнений (необходимое условие условного экстремума) и найти точки 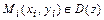возможного условного локального экстремума и соответствующие им значения множителя Лагранжа. 4) Найти выражение второго дифференциала функции Лагранжа 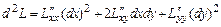в точках при условии, что и 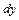связаны уравнением . 5) Сделать вывод о наличии экстремумов функции приусловии , используя достаточное условие условного экстремума. Если для всех , (одновременно), связанных уравнением 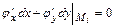, , 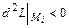то в точке - локальный максимум; если 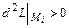, то в точке - локальный минимум. Если 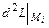принимает как положительные, так и отрицательные значения, то в точке экстремума нет. 6) Найти локальные условные экстремумы функции .