
Читайте также:
|
1) Находим область определения функции  .
.
2) Составляем функцию Лагранжа: 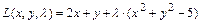 .
.
3) Записываем необходимое условие условного экстремума  ,
,
где:  ,
,
 . Получим
. Получим 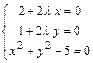 . Решая систему, находим две точки возможного условного экстремума функции
. Решая систему, находим две точки возможного условного экстремума функции  вобласти
вобласти  и соответствующие им значения множителя Лагранжа
и соответствующие им значения множителя Лагранжа  :
: 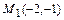 при
при 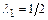 и
и  при
при  .
.
4) Находим выражение второго дифференциала функции Лагранжа



 .
.
Вычисляем 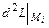 при условии
при условии 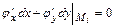 , учитывая, что:
, учитывая, что:
 ;
;
 .
.
Получим:



 ;
;

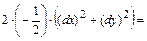
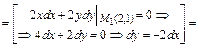
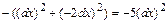 .
.
5) Делаем вывод о наличии экстремумов. Так как для всех  :
: 
 , то в точке
, то в точке  - условный локальный минимум;
- условный локальный минимум;
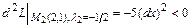 , то в точке
, то в точке  - условный локальный максимум.
- условный локальный максимум.
6) Находим условные минимум и максимум функции  при условии
при условии 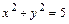 :
:
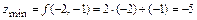 ,
, 
Ответ:  ,
,  при условии
при условии 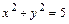 .
.
10.1–30. Найти наибольшее и наименьшее значения функции:
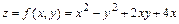 в области D:
в области D:
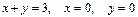
Функция  , дифференцируемая в ограниченной замкнутой области
, дифференцируемая в ограниченной замкнутой области 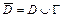 , достигает своего наибольшего и наименьшего значений или в стационарных точках
, достигает своего наибольшего и наименьшего значений или в стационарных точках  , или в точках границы
, или в точках границы  области
области 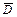 . Для их нахождения необходимо: 1) Найти все стационарные точки
. Для их нахождения необходимо: 1) Найти все стационарные точки  функции и вычислить в них значения функции
функции и вычислить в них значения функции  . 2) Найти наибольшее
. 2) Найти наибольшее 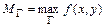 и наименьшее
и наименьшее 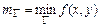 значения функции на границе
значения функции на границе  , задаваемой одним аналитическим выражением в явном виде
, задаваемой одним аналитическим выражением в явном виде  или
или  . Если
. Если  , где
, где 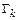 задаются одним аналитическим выражением в явном виде, то находят наибольшие и наименьшие значения
задаются одним аналитическим выражением в явном виде, то находят наибольшие и наименьшие значения  и
и 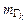 функции на каждом из участков
функции на каждом из участков 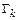 границы. 3) Сравнить значения функции
границы. 3) Сравнить значения функции  ,
,  ,
, 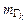 и выбрать из них наибольшее
и выбрать из них наибольшее  и наименьшее
и наименьшее  значения функции в области
значения функции в области 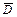 .
.
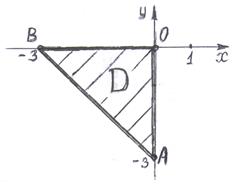
Решение. Изображаемобласть 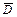 (она представляет собой треугольник, ограниченный прямыми
(она представляет собой треугольник, ограниченный прямыми 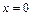 ,
, 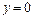 ,
,  ), находим стационарные точки
), находим стационарные точки  функции
функции  , решаясистему уравнений
, решаясистему уравнений
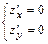 , и вычисляем в них значения функции
, и вычисляем в них значения функции  .
.
Учитывая, что:  ,
, 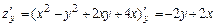 , получим
, получим  . Отсюда
. Отсюда  ,
,  и, следовательно, единственной стационарной точкой функции в области
и, следовательно, единственной стационарной точкой функции в области 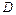 является точка
является точка 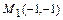 .
.
Вычислив значение функции в этой точке, получим  .
.
2) Границу  области
области 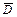 представляем в виде
представляем в виде  , где
, где 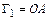 :
: 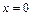 ,
,  ;
;  :
: 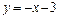 ,
, 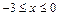 ;
; 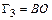 :
: 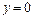 ,
, 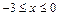 и находим наибольшие и наименьшие значения функции на каждом из участков границы:
и находим наибольшие и наименьшие значения функции на каждом из участков границы:  ,
,  ,
,  ,
,  ,
,  ,
, 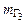 .
.
На участке 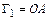 :
: 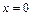 ,
,  :
:  . Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменной
. Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменной 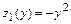 на отрезке
на отрезке 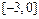 . Эти значения функция принимает или в критических точках, принадлежащих интервалу
. Эти значения функция принимает или в критических точках, принадлежащих интервалу  или на концах отрезка. Для их отысканиянаходим первую производную функции:
или на концах отрезка. Для их отысканиянаходим первую производную функции: 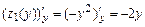 и определяем её внутренние критические точки, т.е. точки
и определяем её внутренние критические точки, т.е. точки 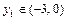 в которых
в которых 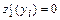 или
или  не существует:
не существует: 
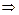
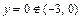 , точек
, точек 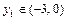 в которых
в которых  не существует нет. Вычисляем значения функции
не существует нет. Вычисляем значения функции 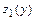 во внутренних критических точках (таких точек нет) и на концах отрезка
во внутренних критических точках (таких точек нет) и на концах отрезка 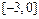 :
: 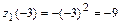 ,
,  . Сравнивая значения
. Сравнивая значения  ,
,  находим наименьшее и наибольшее значения функции
находим наименьшее и наибольшее значения функции 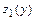 на отрезке
на отрезке 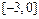 :
:  ,
,  .
.
На участке  :
: 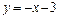 ,
, 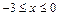 :
:  . Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменной
. Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменной 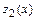 на отрезке
на отрезке 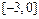 . Эти значения функция принимает или в критических точках, принадлежащих интервалу
. Эти значения функция принимает или в критических точках, принадлежащих интервалу  или на концах отрезка. Для их отысканиянаходим первую производную функции:
или на концах отрезка. Для их отысканиянаходим первую производную функции:  и определяем её внутренние критические точки, т.е. точки
и определяем её внутренние критические точки, т.е. точки  в которых
в которых  или
или  не существует:
не существует: 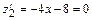
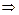
 , точек
, точек  в которых
в которых  не существует нет. Вычисляем значения функции
не существует нет. Вычисляем значения функции 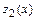 во внутренних критических точках и на концах отрезка
во внутренних критических точках и на концах отрезка 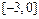 :
:  ,
,  ,
, 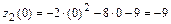 . Сравнивая значения
. Сравнивая значения  ,
, 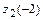 ,
,  находим наименьшее и наибольшее значения функции
находим наименьшее и наибольшее значения функции 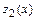 на отрезке
на отрезке 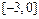 :
: 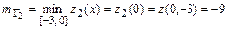 ,
,  .
.
На участке 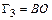 :
: 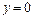 ,
, 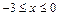 :
: 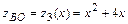 . Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменной
. Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменной  на отрезке
на отрезке 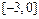 . Эти значения функция принимает или в критических точках, принадлежащих интервалу
. Эти значения функция принимает или в критических точках, принадлежащих интервалу  или на концах отрезка. Для их отысканиянаходим первую производную функции:
или на концах отрезка. Для их отысканиянаходим первую производную функции:  и определяем её внутренние критические точки, т.е. точки
и определяем её внутренние критические точки, т.е. точки  в которых
в которых 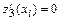 или
или 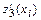 не существует:
не существует: 
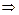
 , точек
, точек  в которых
в которых  не существует нет. Вычисляем значения функции
не существует нет. Вычисляем значения функции 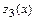 во внутренних критических точках и на концах отрезка
во внутренних критических точках и на концах отрезка 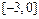 :
: 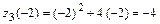 ,
,  ,
, 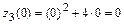 . Сравнивая значения
. Сравнивая значения  ,
,  ,
, 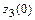 находим наименьшее и наибольшее значения функции
находим наименьшее и наибольшее значения функции 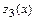 на отрезке
на отрезке 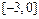 :
: 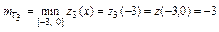 ,
, 
3) Сравнивая значения функции 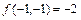 ,
,  ,
, 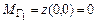 ,
, 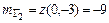 ,
,  ,
,  ,
, 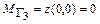 , делаем вывод, что
, делаем вывод, что 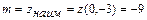 ,
,  .
.
Ответ: 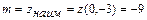 ,
,  .
.
11.1 – 30. Н айти: а) координаты градиента функции 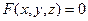 в точке
в точке  ; б) уравнения касательной плоскости и нормали к поверхности, заданной уравнением
; б) уравнения касательной плоскости и нормали к поверхности, заданной уравнением 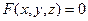 в точке
в точке  .
.
Дата добавления: 2015-07-25; просмотров: 37 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Найти условные экстремумы функции приусловии . | | | Решение. |