Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Решение. Градиент находится по формуле

Для указанной функции требуется: найти а)полный дифференциал ; б) смешанную производную . | Раздел I..Дифференциальное исчисление функции одной переменной. | Раздел II. Функции нескольких переменных. | Семестр 2. | Решение. | А) ; б) ; в) . | Решение. | Ответ: а) ,б) . | Решение. | Найти условные экстремумы функции приусловии . |


Читайте также:
  1. Будь любезен, подумай хорошо, прежде чем принимать решение. Я не намерен терпеть твои перепады настроения и все такое. У меня, в конце концов, может не выдержать сердце.
  2. Глава 21. Решение.
  3. Задача 3. Дифференциальные уравнения с разделяющимися переменными. Найти общее решение.
  4. И тогда, Мудрейший отец, глава клана, принял решение. Он решил отправиться туда, где еще сохранились чистокровные фаэны. В Атлантиду.
  5. Принимаем осознанное решение.
  6. Решение.
  7. Решение.

Градиент 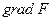находится по формуле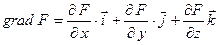

 

а) Найти градиент функции в точке P(1,1,1). В данном случае .

Найдем частные производные функции и вычислим их значения в точке :

;

.

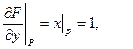
Итак,

Ответ: а)

б)

Уравнение касательной плоскости к поверхности , заданной неявным уравнением , в точке имеет вид: , а уравнение нормали – вид .

Дата добавления: 2015-07-25; просмотров: 37 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Решение.| Краткие теоретические сведения.
mybiblioteka.su - 2015-2024 год. (0.005 сек.)