Читайте также:
|
Тема 1. Производные и дифференциалы функции одной переменной.
Приращением функции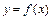 
в точке 
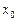, соответствующим приращению аргумента 
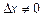называется выражение 
.
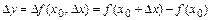Производной 1-ого порядка функции 
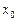в точке называется конечный предел 
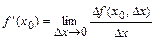. Геометрический смысл производной состоит в том, что число 
равно угловому коэффициенту касательной к графику функции 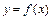в точке 
: 
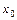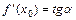, где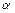 
- угол наклона касательной к оси 
прямоугольной декартовой системы координат 
.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Необходимым условием дифференцируемости в точке является непрерывность функции в данной точке.
Если функция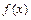 
непрерывна в точке 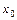и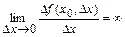 
, то говорят, что в точке 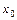функция 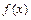имеет бесконечную производную. В этом случае касательная к графику функции 
в точке 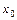перпендикулярна к оси .
Числа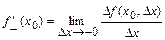 
и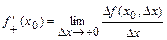 
называются, соответственно левой и правой производными функции в точке 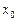. Условие 
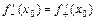равносильно дифференцируемости функции 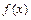в точке 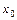, при этом 
.
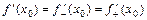Любая элементарная функция дифференцируема во всякой внутренней точке 
естественной области определения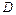 
функции 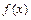, в которой аналитическое выражение её производной 
имеет смысл. Производная 
, рассматриваемая на множестве тех точек , где она существует, сама является функцией. Операция нахождения производной называется также дифференцированием функции .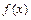
Дата добавления: 2015-07-25; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Основные правила дифференцирования элементарных функций. |