Непрерывность и разрывы монотонной функции

Рассмотрим функцию f (x), которая, – при изменении х в промежутке Р – монотонно возрастает (убывает) хотя бы в широком смысле (гл.1, §4, п.4.4). По отношению к таким функциям имеет место следующая теорема.

Теорема 1. Монотонно убывающая (возрастающая) функция f (x) может иметь в Р разве лишь разрывы первого рода, т.е. скачки.

Возьмем любую точку х ₀ промежутка Р, и пусть она не является левым концом этого промежутка. Рассматривая ту часть промежутка, которая лежит влево от х ₀, применим к ней теорему 12 из §6, п.6.3 о пределе монотонной функции: поскольку для х < х ₀, очевидно, f (x) ≤ f (x ₀), то существует конечный предел .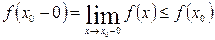

Если он совпадает со значением f (x ₀), то слева в точке х ₀ функция непрерывна; в противном случае – налицо скачок.

Аналогично убеждаемся в том, что в каждой точке х ₀ промежутка Р (не служащей правым его концом) справа тоже либо имеет место непрерывность, либо скачок.

С помощью доказанной теоремы легко установить критерий непрерывности монотонной функции.

Теорема 2. Если значения монотонно возрастающей (убывающей) в промежутке Р функции f (x) содержатся в промежутке Е и сплошь заполняют его (так что каждое значение у из Е принимается функцией хоть раз), то эта функция непрерывна в Р.

Допустим, что в какой-нибудь точке х ₀ из Р функция f (x) имеет разрыв, например, слева; как мы видели, этот разрыв может быть только скачком. В этом случае существует предел f (x ₀ – 0), но он меньше значения f (x ₀). Так как для будет а для очевидно, то функция не может принимать значений у, лежащих между числами и f (x ₀), принадлежащих промежутку Е. Это противоречит условию теоремы; значит, функция разрывов не имеет.

Дата добавления: 2015-07-20