Например, рассмотрим функцию

Эта функция определена для всех х Î R, но в точке х = х ₀ = 0 имеем:

f (x ₀) = 0,

и, следовательно,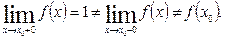

Таким образом, функция sign x в точке x ₀ = 0 как справа, так и слева, имеет разрывы первого рода и, поскольку , то точка x ₀ является точкой неустранимого разрыва: . Скачки функции в точке x ₀ справа и слева равны: 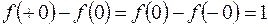. Скачок же функции в точке x ₀ составляет: .

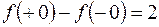2. Функция определена в окрестности точки x ₀, но для нее:

а) не существует как односторонних, так и, следовательно, общего предела функции в точке x ₀;

б) пределы существуют, но равны бесконечности:

– разрыв справа; – разрыв слева;

– разрыв и справа, и слева.

Такие разрывы функции называют разрывами второго рода.

В качестве примера рассмотрим функцию

Эта функция определена для всех х Î R. Найдем односторонние пределы в точке х = х ₀ = –2.

,

.

Отсюда следует, что в точке х ₀ = –2 справа – разрыв второго рода , а слева – непрерывность .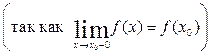

3. Точка х ₀ не принадлежит области определения функции, т.е. функция в этой точке не определена. В этом случае если х ₀ есть внутренняя точка области определения функции, то функция имеет разрывы как справа, так и слева от точки х ₀.

Рассмотрим две функции . Обе функции не определены в точке х ₀ = 0. Следовательно, точка х ₀ = 0 является точкой разрыва данных функций.

Для первой из них имеем: 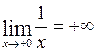и . Это означает, что в точке х ₀ = 0 разрыв второго рода с обеих сторон. Для второй же –

,

в точке х ₀ = 0 – с обеих сторон скачки, т.е. разрывы первого рода.

Дата добавления: 2015-07-20