|
Читайте также: |
(1.22)
будут, очевидно, высшего порядка, чем х.
Заметим, что если бесконечно малая f (x) оказывается высшего порядка, чем бесконечно малая y (x), то этот факт записывают так: 
. Например, можно писать: 
и т.п. Таким образом, символ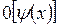 
служит общим обозначением для бесконечно малой высшего порядка, чем y (x).
Для более точной сравнительной характеристики поведения бесконечно малых вводят шкалу сравнения бесконечно малых функций, обеспечивающей выражение порядков их – числами.
Определение 1. Уславливаются считать бесконечно малую функцию f (x) бесконечно малой к -го порядка малости относительно бесконечно малой функции y (x) при х ® х 0, если f (x) и 
будут бесконечно малыми одного порядка малости, т.е. если 
.
Теперь, например, можно, не довольствуясь утверждением, что бесконечно малые (1.22) (при х ® 0) будут бесконечно малыми высшего порядка малости, чем y (x) = х, сказать точно, что первые две из них суть бесконечно малые второго порядка, а последняя – третьего порядка малости относительно y (x) = х, ибо
.
Остановимся теперь на одном особенно важном частном случае бесконечно малых одного порядка.
Определение 2. Две бесконечно малые функции f (x) и y (x) при х ® х 0 называются эквивалентными, если их разность g (x) = f (x) – y (x) оказывается бесконечно малой функцией более высокого порядка малости, нежели они сами.
Установим полезный критерий эквивалентности двух бесконечно малых, который, в сущности, дает второе определение этого понятия, равносильное данному ранее:
Для того, чтобы две бесконечно малые функции f (x) и y (x) были эквивалентны, необходимо и достаточно, чтобы предел их отношения при х ® х 0 был равен единице, т.е. 
.
Эквивалентность функций f (x) и y (x) при х ® х 0 обозначают f (x) ~ y (x).
Основные свойства эквивалентности бесконечно малых функций сводятся к следующим:
1. 
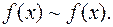
2. Если 
то 
3. Если 
и 
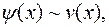то 
4. При достаточно малых значениях 
и 
можно со сколь угодно большой относительной точностью положить = . На этом основана, при приближенных выкладках, замена сложных бесконечно малых эквивалентными им простыми.
Так, например, при раскрытии неопределенности вида 
, т.е. при разыскании предела отношения двух бесконечно малых функций 
, при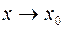 
, каждая из них при этом может быть заменена, без влияния на предел, любой эквивалентной ей бесконечно малой функцией. Действительно, если 
и 
, т.е. 
и 
, то
.
Примеры. 1. Найти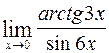 
. Поскольку 
и 
при 
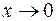, то
2. Найти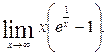 
При 
, 
Тогда,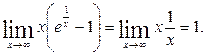 
Дата добавления: 2015-07-20; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сравнение бесконечно малых | | | Классификация бесконечно больших |