|
Читайте также: |
Пусть функции f (x) и y (x) определены и не равны нулю в некоторой окрестности точки х 0. Кроме того, при х ® х 0 они являются бесконечно малыми, т.е. 
.
Во многих случаях представляет интерес сравнение названых бесконечно малых между собой по характеру их приближения к нулю. В основу сравнения двух бесконечно малых f (x) и y (x) кладется поведение их отношения.
Если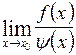 
существует, то бесконечно малые f (x) и y (x) называются сравнимыми, если же этот предел не существует, то бесконечно малые f (x) и y (x) называются несравнимыми. Например, если взять y (x) = х и 
, то их отношение, равное 
при х ® 0 предела не имеет и, следовательно, такие две бесконечно малые несравнимы между собой.
Для сравнимых бесконечно малых функций устанавливаются следующие два соглашения:
1. Если отношение 
(а с ним и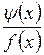 
) имеет конечный и отличный от нуля предел при х ® х 0, то бесконечно малые f (x) и y (x) считаются бесконечно малыми одного порядка малости:
.
2. Если же отношение 
стремится к нулю (а отношение 
– к ∞) при х ® х 0, то бесконечно малая f (x) считается бесконечно малой высшего порядка малости, чем бесконечно малая y (x), и одновременно бесконечно малая y (x) будет низшегопорядка малости, чем бесконечно малая f (x).
Например, если y (x) = х (х 0 = 0), то по сравнению с этой бесконечно малой одного порядка с нею будут и бесконечно малые 
, ибо, как мы знаем (§6, п.6.4),
.
Дата добавления: 2015-07-20; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Примеры на нахождение пределов для некоторых неопределенных выражений | | | Наоборот, бесконечно малые |