
Читайте также:
|
Естественно встает вопрос о распространении теории пределов, развитой в предыдущем параграфе применительно к случаю последовательности на рассматриваемый здесь общий случай произвольной числовой функции одного действительного переменного.
Для этого можно было бы все теоремы о последовательностях, имеющих предел, и рассмотренные нами в §5, доказать аналогичным образом заново для функций. Однако в этом нет необходимости, так как если, говоря о пределе функции, стоять на «точке зрения последовательностей» (определением предела по Гейне), то, поскольку для последовательностей теоремы доказаны, они верны и для функций.
Следовательно, получаем утверждения:
1. Если функция имеет предел в точке х 0, то он единственный.
2. Если при стремлении х к x 0 функция f (x) имеет конечный предел l, то для значений х, достаточно близких к х 0, функция f (x) будет ограниченной:
 .
.
Переходя к другим теоремам, в которых функции связываются знаками равенства, неравенства или арифметических действий, мы, прежде всего, должны оговорить, что, соединяя две или несколько функций f (x), g (x),… (определенных в одной и той же области Р) такими знаками, мы всегда подразумеваем, что их значения отвечают одному и тому же значению х.
3. Выполняется теорема 3, а также теорема Гурьева (гл.1, §5, п.5.2). Если  и
и  , то
, то  .
.
4. Сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
5.Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
6. Для того, чтобы число l было пределом функции y = f (x) при х ® х 0, необходимо и достаточно, чтобы разность f (x) – l была бесконечно малой функцией, т.е.  .
.
7. Функция, обратная бесконечно большой функции при х ® х 0 или х ®¥, есть функция бесконечно малая при х ® х 0 или х ®¥ и наоборот.
8. Если существуют пределы 
 то
то

9. При тех же условиях 
10. Если 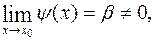 то
то

11. 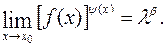
Таким же образом на общий случай, рассматриваемый нами теперь, автоматически переносятся и утверждения, доказанные в §5, п.5.6 и п.5.7 относительно особых случаев. Если известны пределы функций f (x) и ψ (x) (конечные или нет), то на основании этого можно судить о пределах выражений f (x) ± ψ (x), f (x)× ψ (x),  и
и  во всех случаях, кроме семи, условно характеризуемых символами
во всех случаях, кроме семи, условно характеризуемых символами 
 ,
,  ,
,  ,
,  , 00,
, 00, 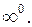 В этих же случаях упомянутые выражения представляют неопределенность, для раскрытия которой уже недостаточно знать лишь пределы функций f (x) и ψ (x), а нужно учесть и самый закон изменения этих функций.
В этих же случаях упомянутые выражения представляют неопределенность, для раскрытия которой уже недостаточно знать лишь пределы функций f (x) и ψ (x), а нужно учесть и самый закон изменения этих функций.
Отметим, что, как и для последовательности,  предел функции
предел функции 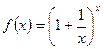 при
при  ∞ также равен е, т.е.
∞ также равен е, т.е. 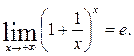
Однако для функции можно установить более общий результат:
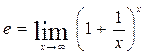 . (1.18)
. (1.18)
Для этого достаточно доказать, что порознь имеют место соотношения
 и
и 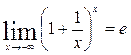 .
.
Покажем, что если выполняется первое соотношение, то верно и второе. Для доказательства введем переменную  . Поскольку при х ® –∞ имеем t = +∞, тогда
. Поскольку при х ® –∞ имеем t = +∞, тогда

Заменим теперь в выражении  переменную х на
переменную х на  если, придать z последовательность значений, стремящихся к нулю (но не равных нулю), то
если, придать z последовательность значений, стремящихся к нулю (но не равных нулю), то 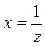 будет стремиться к ∞. Поэтому формулу (1.18) можно переписать в виде
будет стремиться к ∞. Поэтому формулу (1.18) можно переписать в виде
 . (1.19).
. (1.19).
12. Аналог теоремы о сходимости монотонной последовательности.
Пусть функция f (x) монотонно возрастает, хотя бы в широком смысле, в области Р, имеющей точкой сгущения число х 0, большее всех значений х (оно может быть конечным или равным +∞). Если при этом функция ограничена сверху: f (x) ≤ μ (для всех х из Р), то при х → х 0 функция имеет конечный предел; в противном случае – она стремится к +∞.
Предоставляем читателю преобразовать эту теорему для случая, когда предельное значение х 0 меньше всех значений х, равно как и для случая монотонно убывающей функции.
13. Общий признак сходимости (распространение теоремы Больцано-Коши на общий случай).
Для того чтобы функция f (x) при стремлении х к х 0 вообще имела конечный (бесконечный) предел, необходимо и достаточно, чтобы для каждого числа ε > 0 существовало такое число δε > 0, чтобы неравенство  выполнялось, лишь только
выполнялось, лишь только 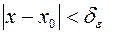 и
и 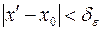 . (для бесконечного предела
. (для бесконечного предела  и
и  ).
).
Дата добавления: 2015-07-20; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение и геометрическое истолкование предела функции | | | Примеры на нахождение пределов для некоторых неопределенных выражений |