Читайте также:
|
Для бесконечно больших функций может быть развита подобная классификация, как и для бесконечно малых.
1. Две бесконечно большие функции f (x) и y (x) при х ® х 0 считаются бесконечно большими функциями одного порядка, если их отношение 
(а с ним и 
) имеет конечный и отличный от нуля предел при х ® х 0.
2. Если же отношение 
стремится к ∞ (а обратное отношение 
– к нулю) при х ® х 0, то f (x) считается бесконечно большой функцией высшего порядка, чем y (x), и одновременно, y (x) будет бесконечно большой функцией низшего порядка чем f (x).
В случае, когда отношение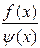 
при х ® х 0 ни к какому пределу не стремится, бесконечно большие функции f (x) и y (x) будут несравнимы.
3. Бесконечно большая функция f (x) называется бесконечно большой k -го порядка относительно бесконечно большой функции y (x) при х ® х 0, если f (x) и 
будут бесконечно большими при х ® х 0 одного порядка, т.е. если
Дата добавления: 2015-07-20; просмотров: 634 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Наоборот, бесконечно малые | | | УПРАЖНЕНИЯ |