
Читайте также:
|
1. Найти пределы функций:
а)  ; б)
; б)  ; в)
; в)  ;
;
г) 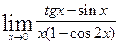 ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ; и)
; и)  ;
;
к)  ; л)
; л)  ; м)
; м)  ;
;
н) 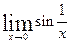 ; о)
; о)  .
.
2. Является ли функция  бесконечно большой, если
бесконечно большой, если 
и бесконечно малой если  при
при  ?
?
3. Доказать, что функции  есть бесконечно большими:
есть бесконечно большими:
а) 
НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
Дата добавления: 2015-07-20; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Классификация бесконечно больших | | | Определение непрерывности функции в точке |