Функции, непрерывные в промежутке

Функция f (x) называется непрерывной слева от точки х ₀, если:

1) функция определена в точке х ₀ и в левой ее полуокрестности;

2) существует предел функции в точке х ₀ слева и этот предел равен значению функции в этой точке:

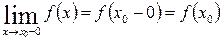. (1.24)

Аналогично определяется непрерывность функции справа от точки х ₀. Условие 2) при этом запишется в виде:

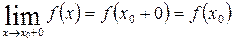(1.25)

Если же х ₀есть внутренняя точка промежутка, т.е. функция f (x) определена как слева, так и справа от точки х ₀, то для того, чтобы выполнялось равенство (1.23), выражающее непрерывность функции в точке х ₀ в обычном смысле, необходимо и достаточно, чтобы имели место оба равенства одновременно: и (1.24), и (1.25). Иными словами, непрерывность функции в точке х ₀ равносильна ее непрерывности в этой точке одновременно справа и слева.

Если функция непрерывна в каждой внутренней точке х интервала (a, b), то такая функция называется непрерывной в интервале (a, b).

Если функция непрерывна в каждой внутренней точке х сегмента [ a, b ], а в концевых точках – для левого конца непрерывна справа, а для правого конца непрерывна слева, т.е.

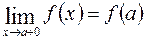и ,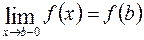

то говорят, что функция у = f (x) непрерывна на сегменте [ a, b ].

График функции, непрерывной в промежутке, представляет собой непрерывную (сплошную) линию на этом промежутке.

Дата добавления: 2015-07-20