Непрерывность сложной функции

Теорема. Пусть функция j (у) определена в промежутке Е, а функция f (х) – в промежутке Р, причем значения последней функции не выходят за пределы Е, когда х изменяется в Р. Если f (х) непрерывна в точке х ₀ из Р, а j (у) непрерывна в соответствующей точке у ₀ = f (х ₀) из Е, то и сложная функция j [ f (х)] будет непрерывна в точке х ₀.

Доказательство. Зададимся произвольным числом > 0. Так как j (у) непрерывна при у = у ₀, то по 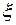найдется такое d > 0, что из | у – у ₀| < d следует

| j (у) – j (у ₀)| < .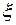

С другой стороны, ввиду непрерывности f (x) при х = х ₀, по d найдется такое s > 0, что из | х – х ₀| < s следует | f (x) – f (x ₀)| = | у – у ₀| < d.

По самому выбору числа d отсюда следует далее

.

Этим "на языке 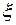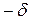" и доказана непрерывность функции 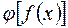в точке х ₀.

Дата добавления: 2015-07-20