Заданной импульсной характеристикой.

Нерекурсивный дискретный фильтр.

Пусть задан аналоговый линейный фильтр, обладающий импульсной характеристикой g(t):

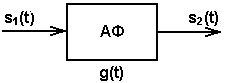
Рис. 5.

Алгоритм работы такого фильтра может быть представлен в виде интеграла свертки:

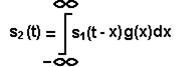(1)

Для построения эквивалентного дискретного фильтра необходимо представить воздействие s₁(t) и импульсную характеристику g(t) в дискретной форме, воспользовавшись разложением в ряд Котельникова В.А. Интервал дискретизации Т соответствует требованиям теоремы Котельникова В.А.

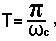
где в качестве ω c следует выбрать наибольшую из граничных частот в спектрах воздействия s₁(t) и импульсной характеристики g(t). Тогда:

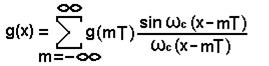(2)

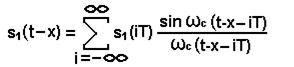(3)

Подставим (2) и (3) в выражение (1) и вычислим значение отклика s₂(t) в момент времени t=nT

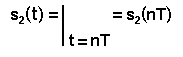
В полученном сложном выражении под интегралом оказываются слагаемые вида:

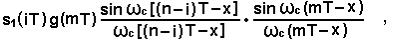
которые содержат произведения ортогональных функций отсчетов. Так как интеграл от произведения «разноименных» ортогональных функций всегда равен нулю, то в выражении для s₂(nТ) следует оставить лишь слагаемые, содержащие одноименные ортогональные функции. В нашем случае это соответствует условию: n-i=m или i=n-m.

Тогда:

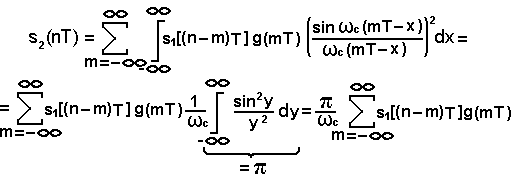
В полученном выражении постоянный множитель 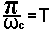не играет принципиальной роли при рассмотрении алгоритма вычисления отсчета отклика s₂(nТ) и в дальнейшем может быть отброшен.

Следовательно, алгоритм работы дискретного фильтра, эквивалентного аналоговому фильтру с заданной импульсной характеристикой g(t), может быть представлен в виде:

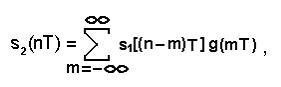(4)

Где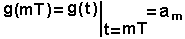

- отсчеты импульсной характеристики аналогового фильтра

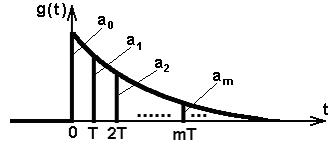
Рис. 6.

Заметим, что для реальных фильтров протяженность функции g(t) является конечной, поэтому число отсчетов импульсной характеристики N будет также конечным ().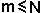

Следовательно, выражение (4) можно переписать в виде:

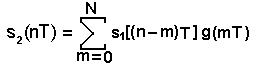(5)

Последнее выражение представляет собой дискретный эквивалент свертки воздействия s₁(t) и импульсной характеристики g(t). Как видно из выражения (5), в формировании каждого очередного отсчета отклика s₂(nТ) принимает участие очередной (текущий) отсчет воздействия s₁(nТ) и N его предыдущих отсчетов: s₁[(n-1)T ], s₁[(n-2)T ], …, s₁[(n-N)T ].

Следовательно, дискретный фильтр, алгоритм которого мы получили, должен обладать памятью, в которой хранится N предыдущих отсчетов воздействия, а также содержатся (N+1) значений отсчетов импульсной характеристики аналогового фильтра {a_m}.

Структурная схема дискретного фильтра, реализующего алгоритм работы (5), может быть представлена в виде:

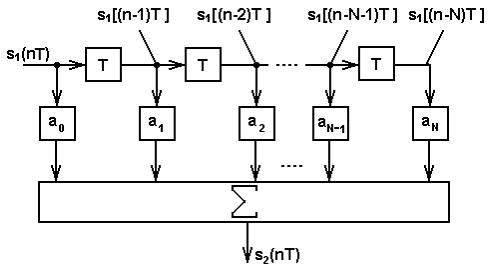
Рис. 7.

На этой схеме применены следующие обозначения:

- идеальный элемент задержки на времяТ     - весовой умножитель с коэффициентом умноженияam     - сумматор

В принципе, структурную схему такого дискретного фильтра, названную нерекурсивным (трансверсальным), можно изобразить по-другому:

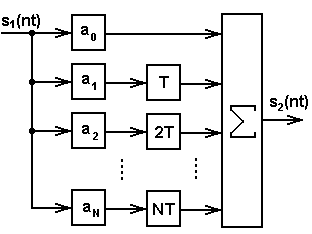
Рис. 8.

Здесь использовано обозначение:

Дата добавления: 2015-07-20