
|
Читайте также: |
Наличие в выражениях, описывающих основные характеристики дискретных сигналов и фильтров, трансцендентных (экспоненциальных) функций вида е-kpT или е-jkωT существенно усложняет анализ прохождения сигналов через дискретные фильтры.
С целью упрощения удобно ввести так называемое Z-преобразование
Z=epT
Тогда выражение
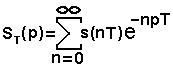
преобразуется в алгебраическое выражение вида

Передаточная функция ДФ также упрощается:
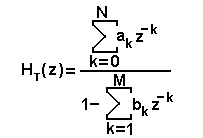
На структурных схемах соответственно идеальный элемент задержки на время kT изображается в виде  .
.
Существует и обратное z-преобразование, при котором находятся временные характеристики

В отличие от понятия передаточная функция ДФ НТ(р), вводится понятие системная функция НТ(z).
Дата добавления: 2015-07-20; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 1. Нерекурсивный дискретный фильтр. | | | Через дискретный фильтр временным методом. |