
Читайте также:
|
Перепишем алгоритм работы (5) дискретного нерекурсивного фильтра (дискретную свертку) в другом виде:
 (7)
(7)
Отклик дискретного фильтра можно выразить через отсчеты s2(nT):
 (8)
(8)
Тогда:
 (9)
(9)
Выражение (9) можно рассматривать как свертку отсчетов воздействия {s1(mT)} и импульсной характеристики дискретного фильтра gT(t). Для реального дискретного фильтра число слагаемых во второй сумме является конечным.
Используя свойства преобразования Фурье, найдем спектральную характеристику отклика дискретного фильтра S 2T(ω)  S2T(t):
S2T(t):
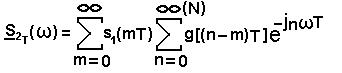 (10)
(10)
Обозначим n-m=k или n+m=k,тогда:

Введенные обозначения означают:
S 1T(ω) – спектральная характеристика воздействия фильтра S1T(t)
Н T(ω) – имеет смысл комплексного коэффициента передачи или передаточной функции дискретного фильтра.
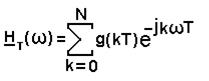 (11)
(11)
Из выражения (11) следует что нерекурсивный дискретный фильтр можно рассматривать как параллельное соединение четырехполюсников с передаточными функциями {ake-jkωT}, где
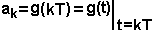
Отсюда получается еще один вариант структурной схемы нерекурсивного дискретного фильтра:

Рис. 10.
| Здесь четырехполюсник вида | 
| отображает идеальный элемент |
| задержки на время kT |
Если вместо преобразования Фурье в выражении (10) использовать преобразование Лапласа, получим соответственно
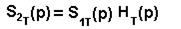 (12)
(12)
| где | 
| - передаточная функция ДФ |
и вариант структурной схемы, изображенный на рис. 11.

Рис. 11.
| Здесь | 
| - идеальный элемент задержки на время kT |
Дата добавления: 2015-07-20; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нерекурсивного дискретного фильтра. | | | И его передаточная функция |