
Читайте также:
|
Если известен алгоритм работы или структурная схем ДФ и известно воздействие на фильтр в виде {s1(nТ)} или
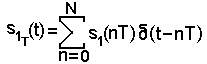
то отклик линейного дискретного фильтра может быть легко найден с помощью принципа суперпозиции: находятся отдельно отклики на каждый отсчет воздействия, а результаты складываются.
Например, для нерекурсивного фильтра
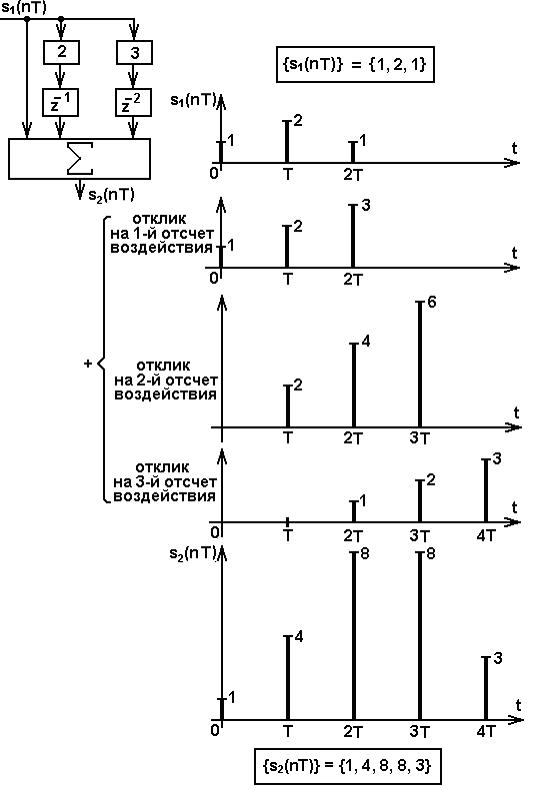
Рис. 18.
Для рекурсивного дискретного фильтра отклик находится аналогичным способом, но в общем случае за счет задержанной обратной связи, отклики на каждый отсчет воздействия имеют неограниченное число отсчетов (для устойчивой работы фильтра они должны постепенно уменьшаться).
Например, для рекурсивного фильтра
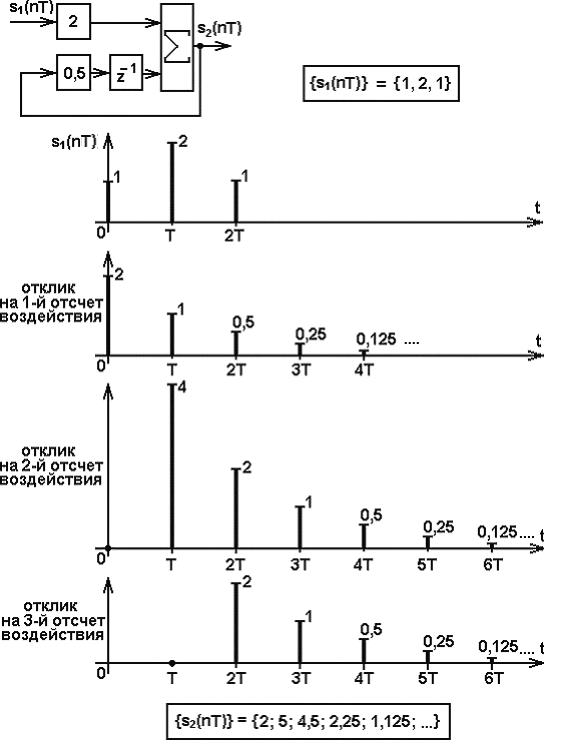
Рис. 19.
Простота анализа прохождения сигнала через ДФ временным методом является лишь кажущейся, так как с увеличением числа отсчетов N трудоемкость вычислений существенно возрастает. Действительно, для нахождения одного отсчета отклика требуется осуществить N операций умножения и N операций сложения. Даже если пренебречь более простыми операциями сложения, остается N операций умножения. Для нахождения отклика фильтра s2Т(t) потребуется еще N умножений. В результате общая трудоемкость оценивается величиной N2. при этом заметим, что для исключения искажений при вычислении дискретной свертки (16) под величиной N следует понимать сумму необходимого числа отсчетов воздействия Ns1 и необходимого числа отсчетов импульсной характеристики Ng, то есть
N = Ns1+ Ng
При анализе прохождения сложных сигналов с большой базой fcTc>>1 число арифметических операций для нахождения отклика ДФ становится настолько большим, что даже при использовании современной элементной базы вычисления в реальном масштабе времени становятся проблематичными. В дальнейшем это объяснит переход к спектральному методу анализа.
Дата добавления: 2015-07-20; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дискретных сигналов и фильтров. | | | И аналоговых фильтров. |