Теорема отсчетов в частотной области.

Сформулируем такую теорему для сигнала, ограниченного по длительности:

1) Спектральная характеристика S (ω) аналогового сигнала s(t), ограниченного по длительности, 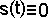при l t l>T_c/2, полностью определяется своими отсчетами { S (k^.ΔΩ)}, взятыми через интервал

2) Значения спектральной характеристики S (ω) при любых значениях частоты ω могут быть найдены в виде суммы ряда

(18)

Если допустить, что исходный аналоговый сигнал s(t) имеет ограниченный спектр (граничная частота ω_с=2π f c), то число слагаемых ряда (18) будет конечным, то есть максимальное значение k_max= ω_с /ΔΩ= f cT и k=0, 1, 2, 3,…, f cT_с

Из свойств преобразования Фурье известно, что значения спектральной характеристики при отрицательных аргументах комплексно сопряжены с соответствующими значениями спектральной характеристики с положительным аргументом

S (-k^.ΔΩ)= S* (k^.ΔΩ)

Поэтому общее число спектральных коэффициентов S (k^.ΔΩ), необходимых для восстановления S (ω), равно f cT_с+1. Так каждый из этих комплексных коэффициентов (кроме нулевого) имеет модуль и аргумент [ S (0) = S(0)], то общее число неизвестных параметров: отсчетов модуля и отсчетов аргумента спектральных коэффициентов, полностью определяющих функцию S (ω),

N=2 f cT_с+1 (19)

Как видим, это число совпадает с необходимым числом отсчетов при временной дискретизации.

§13. Дискретное преобразование Фурье (ДПФ)

Зная теоремы отсчетов в частотной и временной областях, можно ввести понятие дискретного преобразования Фурье, связывающее дискретные отсчеты сигнала s(t) и его спектральной характеристики S (ω).

Пусть дискретный сигнал s_Т(t) получен путем временной дискретизации аналогового сигнала s(t), спектр которого ограничен частотой ω_с=2π f c

(20)

где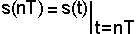

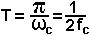
Если сигнал s(t) к тому же ограничен по длительности величиной Т_с, то тогда число слагаемых ряда (20) равно N=2 f cT_с+1.

Спектральная характеристика дискретного сигнала

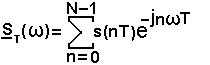(21)

Воспользуемся теоремой отсчетов в частотной области и найдем отсчеты спектральной характеристики (21)

(22)

где

Тогда выражение (22) примет вид:

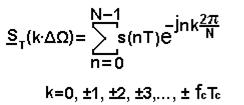(23)

Учитывая, что спектральная характеристика S _Т(ω) – периодическая функция с периодом ω_T=2π/ T можно записать:

S _Т(-k^.ΔΩ) = S _Т[(N-k)^.ΔΩ)]

и оставить только положительные значения k:

k = 0, 1, 2, 3, …, 2f_cT_c = N - 1

Тогда окончательное выражение для S _Т(k^.ΔΩ) = S (k) примет вид:

(24)

Это есть прямое ДПФ.

Аналогично можно получить и обратное ДПФ:

(25)

Заметим, что полученные отсчеты s(n) отличаются от принятых ранее отсчетов s(nТ), тем, что они периодически повторяются на бесконечном интервале времени с периодом N. На рисунке 1 показаны отсчеты s(nТ) и s(n), а также модуль спектральной характеристики дискретного сигнала S_Т(ω) и модули спектральных коэффициентов | S (k)| = S(k).

Рис. 20.

Таким образом, ДПФ устанавливает связь между дискретными отсчетами сигнала во временной и частотной областях {S(n)} и { S (k)}, что удобно при проведении расчетов на ЭВМ.

Дата добавления: 2015-07-20