И его передаточная функция

В рекурсивном дискретном фильтре, в отличие от нерекурсивного, очередной отсчет отклика s₂(nT) формируется не только на основе текущего и N предыдущих отсчетов воздействия, но и на основе нескольких М предыдущих отсчетов отклика т.е.:

(13)

где а_к и b_к – весовые коэффициенты.

В соответствии с алгоритмом (13) работы рекурсивного дискретного фильтра его структурная схема принимает вид, показанный рис. 12.

Рис. 12.

Здесь		- идеальный элемент задержки на время kT
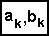
		- весовые умножители

Применяя преобразования Лапласа к выражению (13), найдем изображение

Отсюда передаточная функция рекурсивного дискретного фильтра

может быть записана в виде:

(14)

а структурная схема изображена на рисунке 13:

Рис. 13.

Применяя к выражению (13) преобразование Фурье, получим передаточную функцию рекурсивного дискретного фильтра в виде:

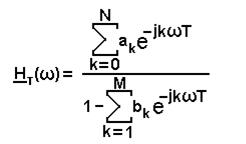(15)

а схему в виде, изображенном на рис. 13 с заменой четырехполюсников на четырехполюсники .

Рассмотрим пример простейшего рекурсивного дискретного фильтра с одним прямым каналом и одним задержанным «обратным» каналом.

Рис. 14.

Передаточная функция этого фильтра:

(16)

Докажем, что этот простейший рекурсивный фильтр эквивалентен нерекурсивному фильтру с бесконечным числом каналов (бесконечной импульсной характеристикой БИХ)

Из математики известно:

Тогда выражение (26) можно переписать в виде:

где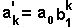

Следовательно, эта передаточная функция соответствует нерекурсивному дискретному фильтру с импульсной характеристикой:

Дата добавления: 2015-07-20