Восстановление дискретизированных сигналов

Соберите схему, приведенную на рисунке 5.6.

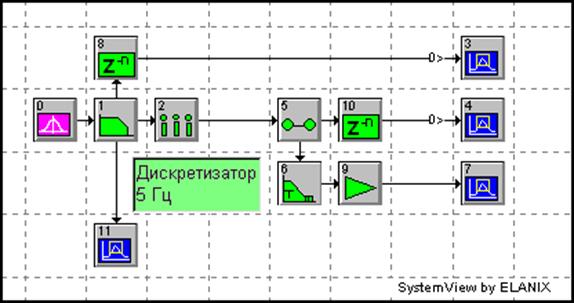
Рисунок 5.6

Установите следующие параметры в системе.

System Time:	0 - 1,022e+1 sec,	dT=2,0e-2 sec,	Sample Rate=5,0e+1 Hz,
Samples=512,	Loops=1
0 Source Gauss Noise	Std Dev = 1 v,	Mean = 0 v,	Max Rate = 50 Hz
1 Operator Linear Sys Butterworth Lowpass IIR,	6 Poles,	Fc = 1 Hz,	Quant Bits =None,
Init Cndtn = Transient	DSP Mode Disabled	MaxRate = 50 Hz
2 Operator Sampler	Non-Interp Right	Rate = 5 Hz	Aperture = 0 sec
Aperture Jitter = 0 sec	Max Rate = 5 Hz
3 Sink Analysis	Input from t8	Output Port 0	Max Input Rate = 50 Hz
4 Sink Analysis	Input from t10	Output Port 0	Max Input Rate = 50 Hz
5 Operator Hold Zero	Gain = 1	Out Rate = 50 Hz	Max Rate = 50 Hz
6 Operator Linear Sys Comm Sin(t)/t FIR	Symbol Rate = 5 Hz	Decimate By 1	Quant Bits = None
Taps = 41	Init Cndtn = Transient	DSP Mode Disabled
Max Rate = 50 Hz
7 Sink Analysis	Input from t9	Output Port 0	Max Input Rate = 50 Hz
8 Operator Smpl Delay	Delay = 20 samples = 400e-3 sec	Attribute = Passive	Initial Condition = 0 v
Fill Last Register	Output 0 = Delay t3	Output 1 = Delay - dT
Max Rate (Port 0) = 50 Hz
9 Operator Gain	Gain = 10	Gain Units = Linear	Max Rate = 50 Hz
10 Operator Smpl Delay	Delay = 20 samples, = 400e-3 sec	Attribute = Passive	Initial Condition = 0 v
Fill Last Register	Output 0 = Delay t4	Output 1 = Delay - dT
Max Rate (Port 0) = 50 Hz
11 Sink Analysis	Input from t1	Output Port 0	Max Input Rate = 50 Hz

Это упражнение иллюстрирует источник случайных помех с ограниченной полосой пропускания 1 Гц (односторонние). Над этим сигналом была произведена выборка с частотой в 5 Гц, а затем он был восстановлен, используя функцию sinc (sin x / x). В уравнении (5.1) показано, что спектр X_s (f) дискретизированного сигнала определяется как:

(5.1)

где X (f) - спектр оригинала недискретизированного сигнала. Как далее показывается в приложении E к учебнику, наиболее качественное восстановление исходного сигнала x (t) из его отсчетов x_s (t) определяется как:

(5.2)

Принимая во внимание формулу 5.2 для числа отсчетов K в модели, мы имеем

(5.3)

a) Выполните моделирование для проверки основных описанных операций. В окне анализа посмотрите на спектр выбранного сигнала и обратите внимание на повторение (копию) спектра, который представлен формулой 5.1.

b) Посмотрите на входной сигнал (с ограниченной полосой шума), дискретизированный сигнал и восстановленный сигнал: является ли исходный и восстановленный сигналы эквивалентными?

c) Обратите внимание, что для идеального восстановления дискретизированного сигнала, как показано в формуле 5.2, требуется идеальная функция sinc, т.е. с бесконечным числом сигналов (taps). Посмотрите на импульсную характеристику функции sinc, используя открывающееся диалоговое окно параметра маркера sinc (маркер 6), и обратите внимание, что конечное число сигналов, это - усеченная sinc форма волны, как показано на рисунке 5.7, так как импульсная характеристика полностью не спадает до нуля.

Рисунок 5.7 – Усеченная sinc форма волны (81 сигнал)

d) Чтобы получать более точное представление о sinc сигнале, число выборок (taps) фильтра sinc должно быть увеличено. Установите параметры функционального модуля 6 следующими:

Operator: Linear Sys - Comm Sin(t)/t FIR
Taps = 501	Quant Bits = None	DSP Mode Disabled
Symbol Rate = 5 Hz	Init Cndtn = Transient	Max Rate = 50 Hz
Decimate By 1

Рисунок 5.8 - Усеченная sinc форма сигнала (501 выборка)

---

Дата добавления: 2015-07-21