Элементы теории графов.

Теория графов – редкий раздел математики, о котором доподлинно известно, когда он родился и кто был его основоположником. Понятие графа было введено Леонардом Эйлером в 1736 году в Санкт-Петербурге в работе, посвященной задаче о Кенигсбергских мостах. Город был расположен на берегах и двух островах реки. Острова и берега реки были связаны между собой семью мостами. Требовалось ответить на вопрос: можно ли, выйдя из дома, вернуться обратно, пройдя по каждому мосту ровно один раз.

a

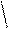
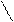
Река

c

b

d

Следующий шаг в развитии теории графов принадлежит Кирхгофу, применившему теорию графов к теории электрических цепей. Сам термин «граф» на 200 лет моложе самой теории. Он введен в 1936 году венгерским математиком Кенигом.

Графы бывают двух видов – ориентированные и неориентированные. Мы будем, в основном, рассматривать ориентированные графы (орграфы, графы).

Графом G называется совокупность двух множеств: вершин V и ребер E, между элементами которых определено отношение инцидентности: каждому ребру e 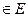поставлена в соответствие пара вершин (u, v) (ребро е инцидентно вершинам u и v). Граф обозначается G=(V, E).

Ориентированные ребраназываются дугами.

Граф, содержащий направленные ребра, называется орграфом.

Ребра, инцидентные одной и той же паре вершин, называются параллельными или кратными. Граф, содержащий кратные ребра, называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным, если множество его элементов (вершин и ребер) конечно, и пустым, если множество его вершин V (а значит и ребер (V)) пусто.

Две вершины называются смежными, если существует хотя бы одно ребро их соединяющее.

Граф изображается в виде диаграммы, на которой вершины изображаются точками, а ребра, соединяющие две вершины, - линиями между этими точками (если граф ориентированный, то на ребре ставят стрелку).

Степенью вершины v называется количество ребер, инцидентных этой вершине. Вершина степени 0 называется изолированно й.

Теорема.

Сумма степеней вершин графа всегда четная и равна 2∙ |E| (удвоенной мощности множества (Е)). (Считается, что вклад петли в степень вершины равен 2).

Граф называется связным, если двигаясь по ребрам, можно из любой его вершины попасть в любую другую.

e₁

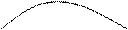
v₁ v₂ v₂ v₃ h

e₂

v₁ v₂

e₃

v₃ v₄ v₁ v₄

неограф без петель. орграф без петель мультиграф с тремя параллельными

ребрами и пет лей

Дата добавления: 2015-07-20