Читайте также:
|
Запись функции в виде СДНФ часто является достаточно длинной. Наша задача состоит в упрощении этой записи. Для эффективного упрощения применим метод Блейка-Порецкого. Метод заключается в попарном склеивании всех элементарных конъюнкций СДНФ между собой, а также полученных в процессе склеивания элементарных конъюнкций меньшего числа переменных. После этого производим поглощение конъюнкциями меньшего числа переменных конъюнкций большего числа переменных.
Для упрощения формул рассматриваются следующие эквивалентные соотношения, выводимые из основных с помощью элементарных преобразований.
1. 
Рассмотрим этот метод на примере
П р и м е р. Упростить СНДФ функции
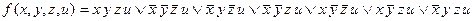
Пронумеруем элементарные конъюнкции СДНФ.
Выполним все попарные склеивания элементарных конъюнкций в СДНФ (под результатом поставим номера склеиваемых конъюнкций):
В качестве упрощения указанных операций рассмотрим алгоритм Куайна.
Допустим известна строка значений функции f(x, y, z).
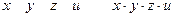
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 0 1 1 1
0 1 0 0 1
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 1
1 0 0 1 0
1 0 1 0 1
1 0 1 1 1
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0
В виде СДНФ функция имеет вид
.
Это сокращенная ДНФ функции. Тупиковая ДНФ функции строится с помощью импликативной матрицы Куайна. Столбцы матрицы идентифицируются элементарными конъюнкциями булевой функции f(x, y, z, u), входящими в СДНФ, а строки – элементарными конъюнкциями, входящими в сокращенную ДНФ. Если заголовок строки является импликантой заголовка столбца, то на пересечении соответствующих строки и столбца ставится крестик. Далее нужно выбрать такое подмножество строк, которые содержат хотя бы один крестик.
(Импликантой булевой функции f называется элементарное произведение, которое равно нулю, во всех тех наборах, где f равна нулю).
Строим таблицу Куайна
Если в столбце только один крестик, то такую строку надо выбрать обязательно; это строка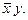 
Далее вычеркиваем столбцы, на пересечении которых с уже выбранной строкой стоят крестики (это столбцы 3, 4, 5, 6). В каждом из оставшихся столбцов стоят два крестика. Множество оставшихся строк имеет четыре подмножества, удовлетворяющих условию чтобы каждый из невычеркнутых столбцов имел крестик хотя бы в одной из строк данного подмножества. Это строки {1, 3, 5}, {1, 3, 6}, {2, 3, 5}, {2, 4, 5, 6}.
Таким образом для рассматриваемой функции имеется четыре тупиковых ДНФ:
Первые три из них являются МДНФ.
Двойственность в алгебре высказываний.
Определение. Пусть f(x1, x2,... xn) – формула алгебры высказываний. Двойственной к ней будем называть формулу f *(x1, x2,... xn), определенную следующим соотношением
f *(x1, x2,... xn ) 
.
Из закона двойного отрицания следует, что (f * )* ≡ f.
П р и м е р 1. 
Теорема 1 (закон двойственности). Формулы f1(x1, x2,...xn) и f2(x 1, x2,...xn) равносильны тогда итолько тогда, когда равносильныf1 * (x1, x2,...xn) и f2 * (x 1, x2,...xn).
Утвержден6ие. Столбец значений функции f * может быть получен из столбца значений функции f с помощью инвертирования (т.е. переписывания в обратном порядке) и поэлементного отрицания.
П р и м е р 2.Рассмотрим функцию f(x1, x2, x3) ≡ 
из предыдущего параграфа. Получим таблицу истинности формулы f*≡. 
0 0 0 1 1 0 0 0
0 0 1 1 1 0 0 1 
0 1 0 1 0 0 0 0
0 1 1 1 1 0 0 0
1 0 0 0 0 0 1 1
1 0 1 0 0 1 1 1
1 1 0 0 1 0 0 1
1 1 1 0 1 1 1 1
Теорема 2 (принцип двойственности для булевых формул) Двойственная к булевой формуле может быть получена заменой констант 0 на 1, 1 на 0, 
и сохранением структуры формул (т. е. соответствующего порядка действий).
П р и м е р 3. 
Скобка в правой части поставлена для соблюдения порядка действий.
Функции алгебры логики.
В высказываниях нас не интересует содержательная часть, а интересует только значения истинности.(т. е. xi принимают значений только 0 или 1). Множество всех наборов значений истинности высказывательных переменных xi конечно и (составляет 2n наборов) и может быть задано таблично. Например, для f(x1, x2) имеем
x1 x2
0 0
0 1
1 0
1 1
Определение. Пусть E2 = {0, 1}. Булевой функцией (функцией алгебры логики) от n переменных называется отображение f: E2n в E2. Напомним, что
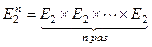
Другими словами.
Определение. Функция f(x1, x2,..., xn) называется булевой (или функцией алгебры логики), если все ее аргументы являются булевыми, а сама функция может принимать только два значения 0 и 1.
Дата добавления: 2015-07-20; просмотров: 121 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Совершенная конъюнктивная нормальная форма. | | | Табличный способ задания. |