Минимизация логических функций с помощью диаграммы Вейча

К наиболее известным систематическим методам минимизации относятся диаграммы Вейча или карты Карно. Этот метод минимизации первоначально предложен Вейчем и усовершенствован Карно.

Минимизация с использованием диаграмм Вейча (карт Карно) имеет следующие этапы:

1. Функцию приводят к дизъюнктивной нормальной форме (ДНФ). Для этого ее необходимо выразить в виде логической суммы простых конъюнкций. Простой конъюнкцией считается логическое произведение переменных, взятых с отрицаниями или без них, в котором каждая переменная встречается не более одного раза. В простую конъюнкцию не должны входить суммы переменных, отрицания функций двух или более переменных.

Простая конъюнкция, в которую входят все аргументы рассматриваемой логической функции, называется минтермом.

Пример правильного минтерма:

Пример запрещенного вида минтерма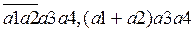

2. После того как исходная логическая функция представлена в ДНФ и произведены очевидные упрощения, следует заполнить прямоугольную таблицу, в которой число клеток равно числу возможных минтермов. Число минтермов зависит от числа переменных i и равно N=2ⁱ, т.е. числу всех возможных сочетаний переменных. При числе переменных равным двум N=4, i=3 N=8 и т.д.

Каждой клетке таблицы ставится в соответствие определенная конъюнкция. Причем делается это таким образом, чтобы в соседних клетках (снизу и сверху, слева и справа) конъюнкции отличались не более чем одним сомножителем.

Затем, используя таблицу истинности, в соответствующую клетку таблицы ставится “1”, если при данном наборе переменных ЛФ = 1 и 0 - если ЛФ = 0 или ничего не ставится, если ЛФ не определена.

3. В заполненной таблице обводят прямоугольными контурами все “1” и затем записывают минимизированную ЛФ в виде суммы логических произведений, описывающих эти контуры. При проведении контуров придерживаются следующих правил:

а) контур должен быть прямоугольным

б) внутри контура должны быть клетки заполненные только единицами

в) число клеток, находящихся внутри контура, должно быть целой степенью числа 2. Т.е. число клеток может равняться 2, 4, 8, 16 и т.д.

г) одни и те же клетки, заполненные единицами, могут входить в несколько контуров

д) при проведении контуров самая верхняя и самая нижняя строки считаются соседними. Тоже - для крайнего левого и крайнего правого столбцов.

е) число контуров должно быть как можно меньшим, а сами контуры - как можно большими.

4. Собственно минимизация. Записываем минимизированную ЛФ как сумму контуров. При этом из обозначения контура исключается переменная, которая изменяется.

Пример 1. Минимизировать с помощью диаграмм Вейча ЛФ Y=

Этап 1. Преобразование к ДНФ.

Используя правило де Моргана (, ) получим

Y=

Получили 3 минтерма для которых Y=1.

Этап 2. Заполнение таблицы.

Для двух переменных диаграмма Вейча содержит 4 клетки, из них 3 содержат “1”, т.е. клетки .(рис. 1-14).

Рис. 1-14

Этап 3. Построение контуров. В диаграмме обводим 2 контура: контур 1 охватывает строку b и 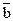, контур 2 - столбец и .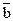

Этап 4. Минимизация ЛФ.

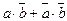В первом контуре () исключаем переменную которая изменяется, т.е. b, остается . Во втором контуре () исключаем a, остается 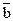. В результате, после минимизации ЛФ равна Y = + .

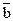Пример 2. Y= 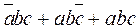. Преобразование выполнялось на предыдущей лекции.

Этап 1. Не выполняется т.к. ЛФ записана в ДНФ

Этап 2. Заполнение таблицы. Число минтермов 8 (N=2ⁱ, i=3). Возможны два варианта таблицы. Таблицы различаются способом обозначения столбцов. При обозначении строк и столбцов должно выполняться следующее правило: при переходе от столбца к столбцу или от строки к стоке в соседних клетках должна изменяться только одна переменная.

Результат преобразования не зависит от порядка обозначения клеток (рис.1-15а, б).

а)

Рис. 1- 15

В контуре 1 а ® , в контуре 2 с® 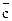, поэтому Y= . Та же ЛФ, что получена на предыдущей лекции, но без длительных преобразований.

Пример 3. Y=

Этап 1. Преобразование к ДНФ. Применив правило де Моргана получим

Y= . В полученной ЛФ имеется не полный минтерм. Для его устранения умножим на ().

Y= .

После заполнения таблицы, обводим два контура (рис. 1-16):

Рис.1- 16

После упрощений получим Y= c + (c - дает к1, - из к2).

Пример 4. Y=

Этап 1. Преобразование к ДНФ.

После заполнения таблицы, обводим три контура (рис. 1-17). Одна клетка изолирована и не попадает ни в один из контуров.

Рис. 1-17

После упрощений, получаем минимизированную логическую функцию:

Y=bd+

Дата добавления: 2015-07-21