Читайте также:
|
1.1 Основные понятия алгебры логики.
Все устройства ЭВМ состоят из элементарных логических схем (ЛС). Работа этих схем основана на законах и правилах алгебры логики или булевой алгебры. Свое название она получила по имени Джорджа Буля - английского математика и логика, заложившего основы математической логики. Джордж Буль родился 2 ноября 1815 года в промышленном городе Линкольне в восточной Англии в семье рабочего. Первые уроки математики получил у отца. В 12 лет знал латынь, затем овладел греческим, французским, немецким и итальянским языками. В 16 лет уже преподавал в деревенской школе, а в 20 открыл собственную школу в Линкольне. В 1847 году он опубликовал работу «Математический анализ логики», в котором высказал идею, что логика более близка к математике, чем к философии. Благодаря этой работе Буль в 1849 году получил пост профессора математики Куинз-колледжа в графстве Корк, несмотря на то, что он даже не имел университетского образования.
В 1854 году опубликовал работу «Исследование законов мышления, базирующихся на математической логике и теории вероятностей». Работы 1847 и 1854 годов положили начало алгебре логики, или булевой алгебре. Буль первым показал, что существует аналогия между алгебраическими и логическими действиями, так как и те, и другие предполагают лишь два варианта ответов – истина или ложь, нуль или единица. Буль изобрел своеобразную алгебру — систему обозначений и правил, применимую к всевозможным объектам, от чисел до предложений. Пользуясь этой системой, он мог закодировать высказывания (утверждения, истинность или ложность которых требовалось доказать) с помощью символов своего языка, а затем манипулировать ими, подобно тому как в математике манипулируют числами. Основными операциями булевой алгебры являются конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ), позволяющих производить сложение, вычитание, умножение, деление и сравнение символов и чисел.
Логические идеи Буля в последующие годы получили дальнейшее развитие. Логические исчисления, построенные в соответствии с идеями Буля, находят сейчас широкое применение в приложениях математической логики к технике, в частности к теории релейно-контактных схем. Например, ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным, либо ложным. В ХХ столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.
В современной алгебре есть булевы кольца, булевы алгебры — алгебраические системы, законы композиции которых берут свое начало от исчисления Буля. В общей топологии известно булево пространство, в математических проблемах управляющих систем — булев разброс, булево разложение, булева регулярная точка ядра.
Необходимо отметить, что дальнейшее развитие булева алгебра получила в работах У.С. Джевонса (Англия), Э.Шредера (Германия), П.С. Порецкого (Россия).
Основные понятия и функции алгебры логики.
Алгебра логики оперирует двумя понятиями: истинности и ложности высказываний. В соответствии с такой двоичной природой высказываний их называют логическими двоичными переменными и обозначают “1” в случае истинности высказывания и “0”, если высказывание ложно. Примерами логических высказываний являются:
А= в неделе 7 дней;
В= сейчас идет лекция;
С= в аудитории идет дождь.
На основании правил алгебры логики можно записать А=1 и В=1, т.к. эти высказывания истинны и С=0 т.к. высказывание ложно - дождя в аудитории нет.
Высказывания могут быть простыми и сложными: простые содержат одно законченное утверждение, сложные образуются из двух или большего числа простых высказываний, связанных между собой некоторыми логическими связями. Преобразование связей между логическими переменными осуществляется в соответствии с правилами алгебры логики.
Две логические переменные А и В, принимающие значения 0 или 1, могут образовывать логические функции. Из 16 возможных функций двух переменных наибольший практический интерес представляют следующие 3 основные функции:
1. Логическое сложение (дизъюнкция) и соответствующая логическая операция ИЛИ;
2 Логическое умножение (конъюнкция) и соответствующая логическая операция И;
3. Логическое отрицание (инверсия) и соответствующая логическая операция НЕ.
Логическая сумма ИЛИ переменных А и В есть логическая функция С, которая истинна, когда хотя бы одна из входных функций истинна.
Операция логического сложения обозначается знаком + или V. В символах алгебры логики логическая сумма записывается так: С = А + В = А V В.
Аналогичное выражение можно записать и для большего числа переменных.
В алгебре логики любые функции удобно изображать в виде таблицы соответствия всех возможных комбинаций, входных логических переменных и выходной логической функции, называемой таблицей истинности. Для логической суммы таблица истинности имеет вид (таблица 1-1):
Таблица 1-1
| А | В | С |
В качестве наглядного примера функции ИЛИ (рис. 1-1) можно привести два и больше контактов, включенных параллельно (здесь и далее положение переключателя принято за входную переменную и замкнутое состояние ключа обозначено логической единицей, а разомкнутое - логическим нулем):
Рис. 1-1
Лампочка будет гореть (событие истинно), если замкнут, хотя бы один из контактов. Электронное устройство, реализующее логическое сложение, называется логическим элементом ИЛИ. Условное графическое изображение логического элемента ИЛИ приведено на рис. 1-2.
Рис. 1-2
Операцию логического сложения следует отличать от операции сложения по модулю два (или в алгебре логики операция «исключающее ИЛИ»). Для этой операции
0 + 0 = 0 1 + 0 =1 1 + 1 = 0
Операцию сложения по модулю 2 обозначают знаком Å. А Å В = С.
Условное графическое изображение логического элемента «исключающее ИЛИ» приведено на рис. 1-3.
Рис. 1-3
Логическое умножение И двух переменных А и В это логическая функция С, которая истинна только тогда, когда одновременно истинны все входные переменные.
Операцию логического умножения обозначают точкой, знаком Ù или никак не обозначают в буквенных выражениях. В символах алгебры логики логическое умножение записывается так: С = А ÙВ = А В.
Для функции логического умножения таблица истинности имеет вид (таблица 1-2):
Таблица 1-2
| А | В | С |
Функцию И наглядно можно представить как последовательное соединение нескольких контактов (рис. 1-4).
Рис. 1-4
Событие истинно (лампа горит) если замкнуты все контакты.
Электронное устройство, реализующее логическое умножение, называется логическим элементом И. Условное графическое изображение логического элемента И приведено на рис. 1-5.
Рис. 1-5
Логическое отрицание НЕ переменной А есть логическая функция В, которая истинна только тогда, когда ложно А, и наоборот.
Логическое отрицание (инверсия) обозначается чертой над обозначением аргумента. При инверсии значение аргумента изменяется на противоположное:
= 1 
= 0
Электронное устройство, реализующее логическое отрицание, называется логическим элементом НЕ. Условное графическое изображение логического элемента НЕ приведено на рис. 1-6.
Рис. 1-6
Двойная инверсия не изменяет значения переменной, т.е. 
= 0 
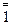= 1
Основываясь на ранее сказанном, можно написать следующие аксиомы, в которых переменная а может принимать значения 0 или 1.
а + 0 = а а + а + а +... + а = а
а + 1 = 1 а × а × а ×... × а = а
а × 0 = 0 а + 
= 1
а × 1 = а а × = 0
= а
Дата добавления: 2015-07-21; просмотров: 245 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПЕНЗА 2009 | | | Основные законы алгебры логики |