
|
Читайте также: |
Правила алгебры логики позволяют преобразовывать логические функции и схемы их реализующие к более простому виду. Например, нам задана логическая функция Y от трех переменных A, B, C (таблица 1-3):
Таблица 1-3
| A | B | C | Y |
Y = 1 при  , ABC, т.е. Y =
, ABC, т.е. Y = 
Для реализации этой функции на логических элементах (рис. 1-7) необходимо: 2 элементе НЕ, 3 элемента И на три входа, 1 элемент ИЛИ на три входа

Рис. 1-7
Преобразуем уравнение к более простому виду
Y =  =
= 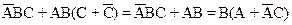
К полученному уравнению применим распределительный закон
Y= 
Возможны две реализации полученных выражений (рис. 1-8):
 |  | ||
Рис. 1-8
Допустим, что для реализации логической функции мы имеем элементы И-НЕ. Применив законы отрицания и двойного отрицания получим (рис. 1-9):

 | |||
 | |||
Рис. 1-9
Дата добавления: 2015-07-21; просмотров: 147 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные законы алгебры логики | | | Понятие функционально полной системы логических элементов |