Читайте также:
|
Для преобразования логических выражений используют следующие законы алгебры логики:
1. Переместительный закон
а + b = b + a ab = ba
2. Сочетательный закон
(a + b) + c = a + (b + c) (ab)c = a(bc)
3.Распределительный закон (имеет две формы)
a(b + c) = ab + bc
a + bc = (a +b)(a + c)
Последнее легко доказывается с помощью алгебраических преобразований:
(a +b)(a + c) = aa + ac + ba + bc = a + ac + ab + bc = a(1 + c + b) = a +bc
4. Закон поглощения
a + ab = a a(1 + b) = a
5. Закон склеивания
ab + a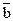 
= a a(b + 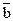) = a × 1 = a
(a + b)(a + 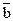) = a aa + a 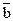+ ab + b 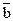= a + a(b + 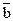) + 0 = a
6. Закон отрицания
= 
× 
= +
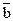
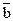
= ab 
= a + b
Закон отрицания называют, так же, законом де Моргана. Он справедлив для любого числа переменных:
= + + 
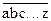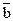Дата добавления: 2015-07-21; просмотров: 87 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Логические основы микропроцессорной техники | | | Применение алгебры логики для упрощения логических функций |