Минимизация логических функций

Целью минимизации логической функции (ЛФ) является уменьшение стоимости ее технической реализации. Минимизация, т.е. отыскание более простого выражения ЛФ, может выполняться различными способами. Например, ЛФ может быть упрощена путем использования алгебраических преобразований, т.е путем выполнения всех возможных операций поглощения, склеивания и т.д в соответствии с законами алгебры логики.

Однако, этот метод требует от разработчика не только глубокого знания возможно большего числа тождеств и аксиом алгебры логики, но и значительной изобретательности и опыта. Основным недостатком этого метода является то, что часто трудно определить является ли полученное выражение минимальным или имеется возможность его дальнейшего упрощения.

Пример. Упростить ЛФ Y =

Объединим 1 и 2 члены:

Y = .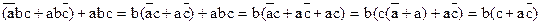

Объединим 1 и 3 члены:

Y = .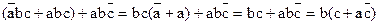

Объединим 2 и 3 члены:

Y = .

Получены три ЛФ, которые проще исходной. Однако, не ясно являются ли полученные функции минимальными. Можно, приняв во внимание, что а + а = а, применить другой способ преобразования. Для этого добавим к функции Y еще один коньюктивный член abc

Y = =

Реализация этой функции требует меньшего числа элементов, чем полученные раньше ЛФ. Очевидно, что полученные ранее ЛФ можно еще больше упростить. Для этого применим распределительный закон a + bc = (a + b)(a + c).

Преобразуем первое уравнение (здесь a= c, b=a, c= ):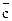

Очевидно, что чем сложнее ЛФ, тем труднее найти путь позволяющий ее минимизировать. Устранить влияние субъективных факторов на процесс минимизации позволяют так называемые систематические методы преобразования ЛФ. Их достоинством является то, что они описываются строгими алгоритмами и для их выполнения может быть использована ЭВМ, что особенно важно при минимизации ЛФ с большим числом переменных

Дата добавления: 2015-07-21