Совершенная конъюнктивная нормальная форма.

Пусть зафиксирован набор булевых переменных x_1, x₂,..., x_n.

Определение 1. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза. Если число переменных равно n, то такая элементарная дизъюнкция называется полной.

В примере 2 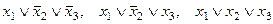- полные элементарные дизъюнкции.

Определение 2. Конъюнкция полных элементарных дизъюнкций называется совершенной конъюнктивной нормальной формой (СКНФ).

Теорема. Любая булева формула может быть представлена и притом единственным образом в виде СКНФ.

Приведение формулы к СКНФ.

Способ перехода от табличного задания к булевой формуле: для каждого набора переменных x₁, x₂,... x_n, для которого функция f(x₁, x₂,... x_n) равна 0, выписывается дизъюнкция всех переменных: над теми переменными, которые на этом наборе равны 1, ставятся отрицания; все такие дизъюнкции соединяются знаком конъюнкции.

Полученная таким образом формула является совершенной конъюнктивной нормальной формой (СКНФ) логической функции f(x₁, x₂,..., x_n).

П р и м е р 1.

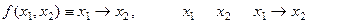
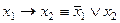
0 0 1

0 1 1

1 0 0

1 1 1

П р и м е р 2.. f(x₁, x₂) ≡ x₁ ~ x₂ x₁ x₂ x₁ ~ x₂ f(x) ≡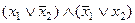

0 0 1

0 1 0

1 0 0

1 1 1

Дата добавления: 2015-07-20