|
Читайте также: |
Пусть w = f(x1, x2,..., xn) - булева функция от n переменных, Область определения можно рассматривать как множество упорядоченных наборов D = {x1, x2,..., xn | xi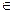 
{0, 1}, i = 1, 2,..., n}, на каждом из которых функция принимает одно из двух значений w = {0, 1}. Количество таких наборов { x1, x2,..., xn} согласно правилу прямого произведения равно
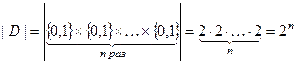
Нетрудно определить и количество всех функций w = f(x1, x2,..., xn).Отдельная функция w = f(x1, x2,..., xn) задана, если заданы значения {w1, w2,... wn} на всех значениях { x1, x2,..., xn} 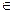D, где wj = {0, 1}- значение функции на j – том наборе { x1, x2,..., xn}. Таких наборов 2n. Отсюда,
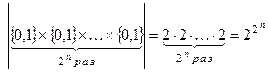
В частности, существуют четыре булевы функции одной переменной.
x f0 (x) = 0 f1(x) =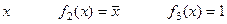 
0 0 0 1 1
1 0 1 0 1
Функции f0 (x), f1(x), f3 (x) называются соответственно нулем, отрицаниям, единицей.
Имеется 16 булевых функций двух переменных
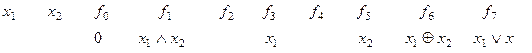
0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1
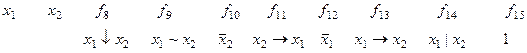
0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1
Названия функций: f1 – конъюнкция, f6 – сложение по модулю 2 (не эквивалентно), f7 – дизъюнкция, f 8 – стрелка Пирса, f9 – эквивалентность или эквиваленция, f13 – импликация, f14 – штрих Шеффера.
В таблице обычно употребляется расположение наборов, соответствующих порядку естественного роста двоичных чисел 0, 1, …, 2n – 1.
Определение. Таблицы, подобные рассмотренным, называются таблицами истинности булевых функций.
Дата добавления: 2015-07-20; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Минимизация ДНФ. | | | Графический способ задания. |