Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Логика предикатов. Кванторы.

Дизъюнкция. | Эквиваленция | Т.е. импликация ложна тогда и только тогда, когда a – истина, а b – ложь. | Формулы алгебры высказываний. | Формулы алгебры высказываний. | Равносильность формул. | Совершенная дизъюнктивная нормальная форма. | Совершенная конъюнктивная нормальная форма. | Минимизация ДНФ. | Табличный способ задания. |


Читайте также:
  1. Анна, существует ли определённая логика в той последовательности, в которой ты проводишь тренинги своего цикла?
  2. ВОДНАЯ ЛОГИКА» И ПАРАЛЛЕЛЬНОЕ МЫШЛЕНИЕ
  3. ГЛАВА. Логика высказываний
  4. ГЛАВА. Логика предикатов
  5. Диалогика
  6. Динамика и логика продуктивного мышления
  7. ДОКАЗАТЕЛЬСТВО И ОПРОВЕРЖЕНИЕ. ЛОГИКА СПОРА

Рассмотрим ряд высказываний: «1 есть простое число», «2 есть простое число», «3 есть простое число»;«4 есть простое число» и т.д. Одни из этих высказываний истинны, другие – ложны, но все они получаются из выражения «n есть простое число», если вместо n подставлять те или иные натуральные числа. Обозначим это выражение через P(n). Само P(n) не является высказыванием, т. к. нельзя сказать истинно оно или ложно, но оно превращается в высказывание при каждом n 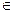N. Выражение такого типа называется одноместным предикатом, определенным на множестве N.

Аналогично, примером двухместного предиката является выражение «x дружит с y», где x и y принадлежат, например, множеству студентов второго курса..

Определение. Пусть x1, x2,..., xn - символы переменных произвольной природы. Эти переменные будем называть предметными. Пусть наборы переменных (x1, x2,..., xn) принадлежат некоторому множеству Ω, которое будем называть предметной областью. Тогда n – местным предикатом, определенным на предметной области Ω, называется отображение Ω во множество высказываний.

Квазиопределение. Связное повествовательное предложение, содержащее n переменных и обладающее следующим свойством: при фиксации значений всех переменных о предложении можно сказать истинно оно или ложно.

Для n – местного предиката существует обозначение P( x1, x2,..., xn), где P - имя предиката.

Определение. Характеристической функцией предиката P( x1, x2,..., xn), определенного на предметной области Ω, называется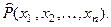

П р и м е р 1. Пусть Ω = {2, 3,..., 8}. Р(x) означает «х – простое число». Таблица истинности этого предиката имеет вид

x P(x)

2 1

3 1

4 0

5 1

6 0

7 1

8 0

П р и м е р 2. Пусть Ω = {1, 2, 3, 4}2 и P(x, y) означает «х является делителем у». Тогда этот предикат можно задать матрицей смежности, которая являетсяфактически таблицей истинности, записанной в более удобном виде

x y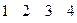

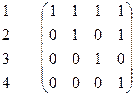
Определение. Если характеристическая функция предиката тождественно равна единице, то такой предикат называется тождественно истинным.

Дата добавления: 2015-07-20; просмотров: 55 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Графический способ задания.| Пример тождественно истинного предиката: .
mybiblioteka.su - 2015-2024 год. (0.006 сек.)