Пример тождественно истинного предиката: .

Пример тождественно ложного предиката: .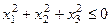

Все операции над высказываниями имеют смысл и для предикатов. Но имеются две важные логические операции, которые имеют именно для предикатов.

Пусть P(x) – одноместный предикат, определенный на области Ω. Поставим ему в соответствие высказывание: «для каждого х Ω Р(х) – истинно». Такое высказывание обозначается 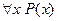и читается «для каждого х имеет место P(x)». Это высказывание истинно тогда и только тогда, когда Р(х) – тождественно истинный предикат.

Определение. Значок называется квантором всеобщности. Говорят, что высказывание 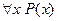получается из предиката Р(х) навешиванием квантора всеобщности.

Составим еще одно высказывание о предикате Р(х) «существует х Ω, для которого Р(х) истинно».Такое высказывание обозначается и читается «существует x, для которого имеет место Р(х). Это высказывание ложно тогда и только тогда, когда Р(х) тождественно ложный предикат.

Определение. Значок называется квантором существования. Говорят, что высказывание получается из предиката Р(х) навешиванием квантора существования.

Обозначения 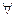и для кванторов – это перевернутые латинские буквы А и Е, которые являются первыми буквами английских слов «All» и «Exist».

Если предметная область Ω конечна Ω ={ a₁, a₂,..., a_k }, то высказывание 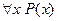равносильно конъюнкции

При этом справедливы обобщенные законы де Моргана

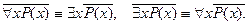
П р и м е р. Ω = N², а Р(х, у) означает «х является делителем у», тогда

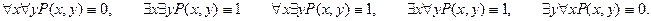
На языке предикатов можно записать многие математические понятия.

Например. Пусть a является пределом последовательности {x_n}. Это означает:

каково бы ни было ε, найдется такое натуральное число N. что для всех n > N выполняется соотношение | x_n – a| < ε. Это высказывание. Существование предела равно истинности этого высказывания. Итак.

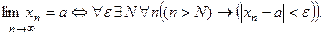
Дата добавления: 2015-07-20