Читайте также:
|
Дано: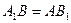 
, 
, 
, 
, 
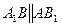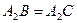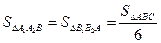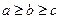(рис 2.2).
Доказать: а) Точка К – центроид 
, б) 
.
Доказательство
1) Проведём 
, 
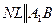(см рис. 2.3.).
2) 
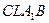- параллелограмм (Так как 
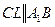и ).
3) Так как 
и 
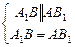, то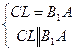 
, значит
— параллелограмм.
4) Так как 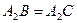, то 
и 
- диагонали 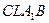, значит 
.
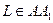5) 
.
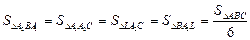
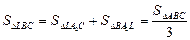6) Так как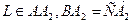 
и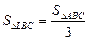 
, то L – центроид 
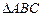, значит
7) В параллелограмме :
.
Так как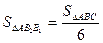 
(по условию) и 
(по доказанному), то 
и L – центроид 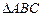, то 
– центроид .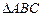
Так как 
и 
параллелограммы, то 
.
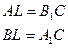Так как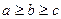 
, то по теореме о принадлежности центроида зонам Дирихле вершин имеем (см. с. 16): 
, что и требовалось доказать.
Дата добавления: 2015-07-25; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 3. | | | Задача 5. |