Центроид

Медиана треугольника ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны (рис. 1.5). Центроид — точка пересечения медиан в треугольнике. Точка пересечения медиан всегда лежит внутри треугольника.

1.3.1. При каких условиях центроид находится на пересечении зон Дирихле всех вершин треугольника?

Как для ортоцентра, центроид принадлежит зонам Дирихле всех вершин треугольника только в равностороннем треугольнике. Это следует из того, что медианы в равностороннем треугольнике являются высотами и центроид совпадает с центром описанной окружности.

1.3.2. При каких условиях центроид

принадлежит зоне Дирихле вершины А?

В треугольнике медиана находится по формуле

, , .

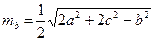Это следует из тождества параллелограмма, согласно которому сумма квадратов диагоналей любого параллелограмма равна сумме квадратов всех его сторон. Известно, что центроидом медианы делятся на отрезки, которые относятся как 2:1, начиная от вершины треугольника. Имеем:

, , .

Будем искать условия на элементы треугольника, при которых , то есть выполняется система .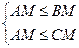

.

Найдем условия на , , 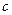при которых эта система верна.

А) Первое неравенство верно тогда, и только тогда, когда

/возведём в квадрат

, ,

, , , выполняется при .

Б) Второе неравенство верно тогда, и только тогда, когда

/возведём в квадрат

, ,

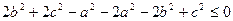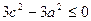, , , выполняется при .

Тогда система выполняется при .

Вывод: .

Дата добавления: 2015-07-25